В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 29

Урок 29. Площади

Домашнее задание из В.В. Ткачук “Математика – абитуриенту”

  1. Точка D лежит между точками A и B (на прямой AB), точка С находится между точками A и D (на той же прямой). Точка M такова, что AM перпендикулярно MD и CM перпендикулярно MB. Известно, что угол CMD равен \(\alpha\) , SAMD = S1, SBMC = S2. Найдите площадь треугольника AMB.
  2. Площадь треугольника ABC равна единице. На стороне BC взята точка A1, а на стороне AC – точка B1. При этом AB1:B1C = p, CA1:A1B=q. Найдите площадь четырехугольника B1CA1K, где K – точка пересечения BB1 и AA1.
  3. Площадь треугольника ABC равна 1. На стороне BC взята точка P, а на стороне AC взяты точки M и N таким образом, что AM:MC=a, MN:NC = b, CP:PB=c. Прямая AP пересекает прямые BM и BN в точках R и S соответственно. Найдите площадь треугольника BRS.
  4. На стороне AB параллелограмма ABCD лежит точка P, а на стороне CD – точка Q, причем AP:PB=p, DQ:QC=q. Диагональ AC пересекает отрезок PQ в точке K. Найдите площадь четырехугольника PKCB, если площадь параллелограмма ABCD равна S.
  5. На стороне AB параллелограмма ABCD, имеющего площадь S, взяты точки P и Q, а на стороне CD – точки R и S, причем AP:PB=p, AQ:QB=q, DS:SC=s, DR:RC=r и p<q, s<r. Отрезки PR и QS пересекаются в точке K. Найдите площадь треугольника KRS.
  6. В трапеции ABCD с основаниями AD и BC на стороне AB взята точка P, а на стороне CD – точка Q, причем AP:PB=p, DQ:QC=q. Площадь трапеции равна S и AD:BC=k. Найдите площадь треугольника PRA, где R – точка пересечения отрезков PQ и AC.
  7. В трапеции ABCD с основаниями AD и BC и имеющей площадь S на стороне AB взяты точки  P и R, а на стороне CD – точки Q и S таким образом, что AP:PB=p, AR:RB=r>p, DS:SC=s, DQ:QC=q>s. Отрезки PQ и RS пересекаются в точке О. Найдите площадь треугольника PRO, если AD:BC = a.
  8. Дан квадрат ABCD. На сторонах AB, BC, CD и AD соответственно выбраны точки P, Q, R, S таким образом, что AP:PB=p, BQ:QC=q, CR:RD=r, DS:SA=s. Отрезки PR и QS пересекаются в точке О. Найдите PO:OR.
  9. Дан квадрат ABCD единичной площади. На стороне AB выбрана точка P, на стороне BC выбрана точки R и S, на сторонах CD и AD – точки Q и T соответственно. Известно, что AP:PB=p, BR:RS=r, BS:SC=s>r, CQ:QD=q, DT:TA=t. Отрезок PQ пересекает отрезки TR и TS в точках M и N соответственно. Найдите площадь треугольника TMN.
  10. В окружность вписан выпуклый четырехугольник ABCD, причем AB – диаметр окружности, и диагонали AC и BD пересекаются в точке M. Известно, что BC = 3, CM = 3/4, SABC=3SACD. Найдите длину отрезка AM.
  11. Дана трапеция ABCD с основаниями AD и BC. Диагонали AC и BD пересекаются в точке О, а прямые AB и CD  – в точке К. Прямая КО пересекает стороны BC и AD в точках M и N соответственно, причем угол BAD равен 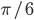\(\pi/6\) и в трапеции ABNM и NMCD можно вписать окружность.  Найдите отношение площади треугольника BKC к площади трапеции ABCD.
  12. В трапеции ABCD основания AD и BC равны 16 и 9 соответственно. На продолжении стороны BC взята точка М такая, что СМ = 3,2. В каком отношении прямая AM делит площадь трапеции ABCD?
  13. В треугольник ABC вписана окружность радиуса R, касающаяся сторон АС, АВ и ВС в точках D, E, F соответственно. Известно, что AD равно R, а DC равно a. Найдите площадь треугольника BEF.
  14. Треугольник ABC вписан в круг, AB = BC, угол ABC равен 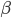\(\beta\). Параллельно AC проведена средняя линия треугольника, продолженная до пересечения с окружностью в точках D и E. Найдите отношение площади треугольника DBE к площади треугольника ABC.
  15. Пусть ABCD – квадрат и точка О лежит вне квадрата, причем OA = OB = 5, OD = 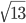\(\sqrt{13}\). Найдите площадь квадрата ABCD.
  16. Известно, что ABCD – ромб и радиусы окружностей, описанных около треугольников ABC и ABD соответственно, равны R и r. Найдите площадь ромба ABCD.
  17. В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найдите площадь трапеции.
  18. Площади треугольников, образованных отрезками диагоналей трапеции с ее основаниями, равны S1 и S2.  Найдите площадь трапеции.
  19. В круг вписан треугольник ABC, в котором AB = BC, угол ABC равен \(\alpha\). Из точки А проведена медиана к стороне BC, пересекающая BC в точке D, а окружность – в точке Е. Найдите отношение площади треугольника ABE к площади треугольника BDE.
  20. В четырехугольнике ABCD имеем AB = BC, AC = CD, угол ACB равен углу ACD. Радиусы окружностей, вписанных в треугольники ABC и ACD, относятся как 3:4. Найдите отношение площадей этих треугольников.

Ответы к домашнему заданию урока 29 из В.В. Ткачук “Математика – абитуриенту”

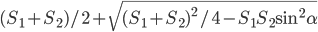
  1. \((S_1+S_2)/2+\sqrt{(S_1+S_2)^2/4-S_1S_2\sin^2\alpha}\)
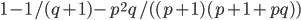
  2. \(1-1/(q+1)-p^2q/((p+1)(p+1+pq))\)
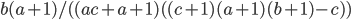
  3. \(b(a+1)/((ac+a+1)((c+1)(a+1)(b+1)-c))\)
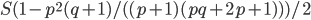
  4. \(S(1-p^2(q+1)/((p+1)(pq+2p+1)))/2\)
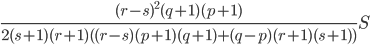
  5. \(\frac{(r-s)^2(q+1)(p+1)}{2(s+1)(r+1)((r-s)(p+1)(q+1)+(q-p)(r+1)(s+1))}S\)
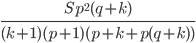
  6. \(\frac{Sp^2(q+k)}{(k+1)(p+1)(p+k+p(q+k))}\)
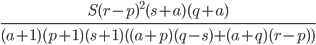
  7. \(\frac{S(r-p)^2(s+a)(q+a)}{(a+1)(p+1)(s+1)((a+p)(q-s)+(a+q)(r-p))}\)
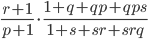
  8. \(\frac{r+1}{p+1}\cdot\frac{1+q+qp+qps}{1+s+sr+srq}\)
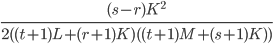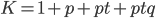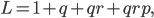
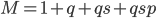
  9. \(\frac{(s-r)K^2}{2((t+1)L+(r+1)K)((t+1)M+(s+1)K))}\), где \(K=1+p+pt+ptq\), \(L = 1+q+qr+qrp,\)\( M = 1+q+qs+qsp\)
  10. 17/4
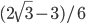
  11. \((2\sqrt{3}-3)/6\)
  12. 7:8
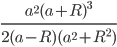
  13. \(\frac{a^2(a+R)^3}{2(a-R)(a^2+R^2)}\)
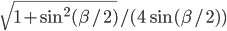
  14. \(\sqrt{1+\sin^2 (\beta/2)}/(4\sin (\beta/2))\)
  15. 2
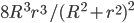
  16. \(8R^3r^3/(R^2+r^2)^2\)
  17. 6
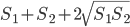
  18. \(S_1+S_2+2\sqrt{S_1S_2}\)
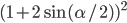
  19. \((1+2\sin (\alpha/2))^2\)
  20. 9/14


Смотрите:

  1. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 9
  2. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 19
  3. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 24
  4. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 14