В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 30

Урок 30. Параллелограммы и трапеции

Домашнее задание из В.В. Ткачук “Математика – абитуриенту”

  1. В параллелограмме ABCD угол C острый, АВ = 3, ВС = 6. Точка  F  лежит на середине стороны AD. Прямая, перпендикулярная к АВ и проходящая через точку С, пересекает продолжение отрезка АВ за точку В в точку Е. Известно, что угол AEF равен \(\alpha\). Найдите площадь четырехугольника AECD.
  2. Площадь трапеции ABCD равна 6, Е – точка пересечения продолжений боковых сторон. Через точку Е и точку пересечения диагоналей проведена прямая, пересекающая меньшее основание ВС в точке Р, а большее основание AD в точке Q. Точка F лежит на отрезке EC, причем EF:FC=EP:EQ=1:3. Найдите площадь треугольника EPF.
  3. В трапеции ABCD диагонали пересекаются под прямым углом, и одно основание ее в два раза больше другого. Отношение длин боковых стороны равно \(m\). Найдите боковые стороны, если сумма квадратов длин диагоналей равна \(d^2\).
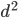  4. В трапеции ABCD основание AD больше основания BC. Известно, что AD = CD = 14/3, угол BAD равен 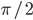\(\pi/2\), угол BCD равен 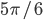\(5\pi/6\). На основании AD построен треугольник AED. Точки B и E лежат по одну сторону от AD и AE = ED. Длина высоты, опущенной из точки Е на прямую AD, равна 7/5. Найдите площадь общей части трапеции ABCD и треугольника AED.
  5. В трапеции ABCE основание AE равно 16. Боковая сторона CE равна 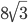\(8\sqrt{3}\). Известно, что окружность, проходящая через точки A, B, C, пересекает сторону AE в точке H, причем угол AHB равен 60о. Найдите BH.
  6. Сторона ромба ABCD равна 6, а угол BAD равен 60о. Точка Е лежит на стороне BC, причем CE = 2. Найдите длину отрезка ОЕ, где О – центр ромба.
  7. В трапеции PQRS основание QR равно 10. Известно также, что QS = 19 и угол QSP равен 30о. Что больше, QR или RS?
  8. Около трапеции KLMN описана окружность. Основание KN трапеции является ее диаметром, причем KN = 4, LM = 2. Хорда MT пересекает KN в точке S такой, что KS:SN=1:3. Найдите площадь треугольника STN.
  9. Дан прямоугольник ABCD, в котором AB = 6, AD = 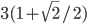\(3(1+\sqrt{2}/2)\). В нем лежат две окружности. Окружность радиуса 2 с центром в точке К касается сторон AB и AD. Окружность радиуса 1 с центром в точке L касается стороны CD и первой окружности. Пусть M – основание перпендикуляра, опущенного из точки B на прямую KL. Найдите площадь треугольника CML.
  10. В трапеции ABCD с основаниями AB и CD диагонали AC и BD пересекаются в точке О, причем треугольник BOC равносторонний. Известно, что АВ = 5, CD = 3. Найдите длину стороны BC.
  11. В трапецию ABCD вписана окружность. Продолжения боковых сторон AD и BC за точки D и C пересекаются в точке Е. Периметр треугольника DCE равен 60, сторона АВ равна 20 и угол ADC равен 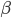\(\beta\). Найдите радиус окружности.
  12. Площадь трапеции ABCD равна 30. Ее основание AD в два раза больше основания BC. Точка P лежит на середине боковой стороны AB, а точка R – на стороне CD, деля ее в отношении DR:RC =2:1. Прямые AR и PD пересекаются в точке Q. Найдите площадь треугольника APQ.
  13. В параллелограмма PQRS биссектриса угла RPQ, равного 80о, пересекает сторону RS в точке L. Найдите радиус окружности, касающийся отрезка PQ и лучей QR и PL, если PQ = 7.
  14. В параллелограмме ABCD биссектриса угла BAD пересекает сторону CD в точке М, причем DM:MC=2:1. Известно, что угол CAM равен \(\alpha\). Найдите угол BAD.
  15. Окружность, проходящая через точку D и касающаяся сторон AB и BC равнобедренной трапеции ABCD, пересекает стороны AD и CD соответственно в точках M и N. Известно, что AD параллельно BC и AB = 7, AD = 6, AM:MD=1:3, CN:ND=4:3. Найдите длину основания BC.
  16. Известно, что ABCD – параллелограмм, BD = 2, угол ACB равен 45о. Прямая CD касается окружности, описанной около треугольника ABD. Найдите площадь параллелограмма ABCD.
  17. Параллелограммы ABCD и A1BCD1 имеют общую сторону BC, причем точка A симметрична A1, а точка D симметрична D1 относительно прямой BC. Отрезки BD и BA1 лежат на одной прямой. Угол между AC и A1C равен 45о. Площадь пятиугольника ADCD1A1 равна 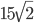\(15\sqrt{2}\). Найдите AB и AD.
  18. Около квадрата BEFC описана окружность радиуса 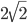\(2\sqrt{2}\). Точка Р лежит на продолжении отрезка DC за точку С, причем PC = 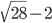\(\sqrt{28}-2\). Через точку Р проведена секущая РА, пересекающая окружность в точках D и A. Известно, что PD = 4 и угол BAC тупой. Найдите угол BPA.
  19. В прямоугольнике ABCD известны длины сторон АВ = 12 и AD = 5. Точка пересечения диагоналей обозначена через Е. Пусть О1 – центр окружности, вписанной в треугольник AED, и О2 – центр окружности, вписанной в треугольник DEC. Найдите EO1:EO2.
  20. [2] В параллелограмме лежат две окружности радиуса 1, касающиеся друг друга и трех сторон параллелограмма каждая. Один из отрезков стороны параллелограмма от вершины до точки касания равен 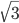\(\sqrt{3}\). Найдите площадь параллелограмма.

Ответы к домашнему заданию урока 30 из В.В. Ткачук “Математика – абитуриенту”

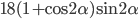
  1. \(18(1+\cos 2\alpha)\sin 2\alpha\)
  2. 3/32
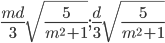
  3. \(\frac{md}{3}\sqrt{\frac{5}{m^2+1}}; \frac{d}{3}\sqrt{\frac{5}{m^2+1}}\)
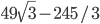
  4. \(49\sqrt{3}-245/3\)
  5. 8
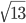
  6. \(\sqrt{13}\)
  7. RS > QR
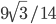
  8. \(9\sqrt{3}/14\)
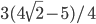
  9. \(3(4\sqrt{2}-5)/4\)
  10. 15/7
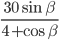
  11. \(\frac{30\sin \beta}{4+\cos \beta}\)
  12. 10/3
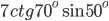
  13. \(7ctg 70^{o}\sin 50^{o}\)
  14. 2arctg(5tg\(\alpha\))
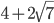
  15. \(4+2\sqrt{7}\)
  16. 4
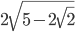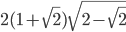
  17. AB = \(2\sqrt{5-2\sqrt{2}}\); AD = \(2(1+\sqrt{2})\sqrt{2-\sqrt{2}}\)
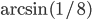
  18. \(\arcsin(1/8)\)
  19. 10/3
  20. \(4+8/\sqrt{3}\)


Смотрите:

  1. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 8
  2. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 41
  3. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 16
  4. В.В. Ткачук Математика – абитуриенту. Домашнее задание к уроку 13