Урок 13. Текстовые задачи. Движение

Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- Переднее колесо повозки на некотором пути сделало на 1000 оборотов больше заднего. Если бы длина окружности переднего колеса была в полтора раза больше, то на том же пути оно сделало бы на 200 оборотов больше заднего колеса. Чему равны длины окружностей колес, если известно, что длина окружности заднего колеса на 1.5 м больше длины окружности переднего колеса? Решение
- Два тела движутся по окружности равномерно и в одну сторону. Первое тело проходит окружность на 2 сек быстрее второго и догоняет второе тело каждые 12 сек. За какое время каждое тело проходит окружность? Решение
- Для того, чтобы из пункта А попасть в пункт В, нужно часть пути от пункта А до пункта С проехать на поезде, а остальные 15 км от С до В - на автобусе. Вся поездка от А до В занимает 1 час 15 мин, причем автобус отправляется сразу после прихода поезда, а временем, которое поезд и автобус тратят на остановки, можно пренебречь. По ошибке пассажир сошел с поезда на остановку раньше, прошел оставшийся путь до С длиной 5 км пешком со скоростью 4 км/ч, а затем еще 20 мин ждал автобуса и в результате попал в пункт В на 1 час 30 мин позже намеченного срока. Найдите расстояние от А до С, если известно, что скорость поезда вдвое больше скорости автобуса. Решение
- [2] Колонна мотоциклистов с интервалом между соседними машинами 50 м движется со скоростью 15 км/ч. В противоположном направлении вдоль колонны (от первой машины) едет велосипедист. Поравнявшись с 45-м мотоциклистом, он увеличивает свою скорость на 10 км/ч, доезжает до последнего мотоциклиста, поворачивает и с той же увеличенной скоростью догоняет первую машину. Если бы велосипедист все время (с самого начала) двигался с этой увеличенной скоростью, то он вернулся бы к голове колонны на 15/8 мин раньше. Найти первоначальную скорость велосипедиста (длина велосипеда, мотоцикла и время поворота велосипедиста не учитываются).
- Пункт А находится на реке выше пункта В. В одно и то же время из пункта А отплыли вниз плот и первая моторная лодка, а из пункта В вверх – вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть АС. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А – первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения равна 3 км/ч ?
- Из города А в город В через равные промежутки времени и с равной скоростью выезжает 21 автобус, каждый из которых проходит путь АВ за 2 ч 40 мин. При этом первый автобус прибывает в город В в тот момент, когда из города А выезжает 21-й автобус. Прибыв в город В, каждый автобус мгновенно разворачивается и движется к городу А. Из города А одновременно с 21-м автобусом выезжает в город В легковая машина, которая через t мин обгоняет 20-й автобус. Найти t и время, за которое легковая машина преодолевает расстояние АВ, если, встретив 1-й автобус, она встречает второй автобус через (t - 9) мин. Автобусы занумерованы в том порядке, в каком они выезжают из города А.
- Города А и В расположены на берегу реки, причем город В лежит ниже по течению. В 9 часов утра из А в В отправляется плот, плывущий относительно берегов со скоростью течения реки. В этот же момент из В в А отправляется лодка, которая встречается с плотом через 5 часов. Доплыв до города А, лодка мгновенно повернула обратно и приплыла в город В одновременно с плотом. Успели ли лодка и плот прибыть в город В к 9 ч вечера того же дня?
- [3] Два бегуна стартовали раздельно в одной точке стадиона в беге на 25 кругов, причем второй начал движение, когда первый прошел полкруга. Один из зрителей вышел со стадиона, когда бегуны были рядом. Когда через 13 мин он вернулся, бегуны снова были рядом. Если бы первый бегун после третьего круга увеличил скорость в 2 раза, а второй бегун после десятого круга – в три раза, то оба бегуна финишировали бы одновременно. Определить, с какой разницей во времени финишировали бегуны, если закончивший бег вторым пробегал за минуту менее круга.
- [2] Из пункта А в пункт В вышел пешеход. Вслед за ним через два часа из пункта А выехал велосипедист, а еще через 30 мин – мотоциклист. Пешеход, велосипедист и мотоциклист двигались равномерно и без остановок. Через некоторое время после выезда мотоциклиста оказалось, что все трое к этому моменту преодолели одинаковую часть пути от А до В. На сколько минут раньше пешехода в пункт В прибыл велосипедист, если пешеход прибыл в пункт В на 1 час позже мотоциклиста?
- Два автобуса выезжают одновременно навстречу друг другу из пункта А и В и встречаются в 12 часов дня. Если скорость первого автобуса увеличить в 2 раза, а скорость второго оставить прежней, то встреча произойдет на 56 мин раньше. Если же увеличить в 2 раза скорость второго автобуса, оставив прежней скорость первого, то встреча произойдет на 65 мин раньше. Определить время встречи, если увеличены вдвое скорости обоих автобусов.
- Из пункта А в пункт В автомобиль доехал за 5 часов, двигаясь в пределах населенных пунктов со скоростью 60 км/ч, а по шоссе вне населенных пунктах – со скоростью 80 км/ч. Обратный путь из В в А занял 4 часа 36 мин. При этом в пределах населенных пунктов автомобиль двигался со скоростью 50 км/ч, а по шоссе – 90 км/ч. Каково расстояние между пунктами А и В?
- [2] Путь из А в В проходит первые 80 км по шоссе, а оставшиеся 120 км - по грунтовой дороге. Первую часть пути автобус проезжает на 2 часа быстрее, чем вторую. Автобус совершил более четырех рейсов по маршруту из А в В и обратно. На это, включая стоянки в конечных пунктах, ушло менее одной недели (то есть менее 168 часов). За время, которое он провел при этом движении, автобус мог бы проехать 2100 км, если бы двигался со скоростью, равной средней арифметической между скоростями движения по шоссе и грунтовой дороге. Найдите скорости движения автобуса по шоссе и по грунтовой дороге.
- [2] В море с прямолинейным берегом впадают две реки с одинаковой скоростью течения. Посередине между их устьями расположен город А, на первой реке находится пункт В, а на второй реке - пункт С. Расстояние вдоль реки от В до устья этой реки равно расстоянию от А до устья реки, а расстояние от С до устья реки составляет 3/4 расстояния от А до устья реки. Из города А одновременно выходят две лодки: первая идет в В (вдоль берега моря и по реке), а вторая идет в С (также вдоль берега моря и по реке). Дойдя до пунктов В и С, лодки сразу поворачивают назад и идут соответственно в пункты С и В. Известно, что общее время, в течение которого первая лодка на пути из А в В, а потом в С шла по морю, относится ко времени, к течение которого она шла по рекам как 45 : 47. Для второй лодки это отношение равно 16 : 17. Какая из лодок первая пришла в свой конечный пункт - первая лодка в С или вторая в В?
- [3] Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 7 часов утра выехал автомобилист, и одновременно с ним из города в село выехал мотоциклист, который двигался по шоссе быстрее, чем по грунтовой дороге в 5/3 раза, а автомобилист – в 3/2 раза (движение обоих по шоссе и по грунтовой дороге считать равномерным). Они встретились в 9 ч 15 мин, автомобилист приехал в город в 11 часов, а мотоциклист приехал в село в 12 ч 15 мин. Определить, сможет ли автомобилист приехать в город до 11 ч 15 мин, если он весь путь из села в город будет ехать с первоначальной скоростью.
- Пункты А и В расположены на одной реке так, что плот, плывущий из А в В, проходит путь от А до В за 24 часа. Весь путь от А до В и обратно моторная лодка проходит не менее, чем за 10 часов. Если бы собственная скорость моторной лодки увеличилась на 40%, то путь от А до В и обратно занял бы у лодки не более 7 часов. Найти время, за которое моторная лодка проходит путь от А до В в случае, когда ее собственная скорость не увеличена.
- Две реки с прямолинейными руслами и одинаковой скоростью течения впадают в одном и том же месте в озере, образуя между собой угол в 60 градусов. От двух причалов, расположенных на разных реках и отстоящих друг от друга на расстоянии 28 км, одновременно вышли байдарка и лодка, скорости которых в стоячей воде соответственно равны 10 км/ч и 3 км/ч. Байдарка достигла озера через 2 часа, лодка через 4 часа. Найти скорость течения рек.
- [2] Автобус проходит путь АЕ, состоящий из отрезков АВ, ВС, СD, DE длиной 10 км, 5 км, 5 км и 6 км соответственно. При этом согласно расписанию, выезжая из пункта А в 9 часов, он проходит пункт В в
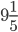 часа, пункт С – в
часа, пункт С – в 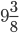 часа, пункт D – в
часа, пункт D – в 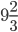 часа. С какой постоянной скоростью v должен двигаться автобус, чтобы сумма абсолютных величин отклонений от расписания прохождения пунктов В, С, D и времени движении автобуса от А до E при скорости v не превосходила 51,7 минут?
часа. С какой постоянной скоростью v должен двигаться автобус, чтобы сумма абсолютных величин отклонений от расписания прохождения пунктов В, С, D и времени движении автобуса от А до E при скорости v не превосходила 51,7 минут? - [2] Согласно расписанию пароход проходит по реке, скорость течения которой 6 км/ч, путь из А в D длиной 18 км за 1 час. При этом, выходя из пункта А в 10 часов, он прибывает в пункты В и С, отстоящие от А на расстоянии 14 км и 17 км соответственно, в 10 часов 12 минут и в 10 часов 18 минут. Известно, что если бы пароход двигался из А в D без остановок с постоянной скоростью v (относительно воды), то сумма абсолютных величин отклонений от расписания прибытия в пункты В, С, D не превышала бы уменьшенного на полчаса времени, необходимого пароходу для прохождения 6 км со скоростью v в стоячей воде. Какой из пунктов А или D находится выше по течению?
- [2] В полночь из пункта А в пункт В по течению реки отправился катер, а из В в А в тот же момент вышла лодка. Лодка была в пути не менее суток. Катер, дойдя до пункта В, сразу повернул назад и возвратился в пункт А не позднее 10 часов 48 минут того же дня. Первая встреча катера и лодки состоялась в 4 часа утра. Найти, когда катер прибыл в пункт В, если его скорость в стоячей воде втрое больше скорости лодки в стоячей воде.
- Из пункта А в пункт В выходит поезд. В момент прибытия этого поезда в В оттуда выходит другой поезд, который следует в А. Время, которое прошло от выхода первого поезда из А до прибытия туда второго поезда, в 25/6 раз превышает время, которое затратили бы поезда до момента встречи, если бы они вышли одновременно из А и В навстречу друг другу. Скорости обоих поездов постоянны, причем скорость второго поезда на 20 км/ч превышает скорость первого поезда. Чему равна скорость каждого поезда?
- Из пункта А в пункт В выезжает автомобиль и одновременно из В в А с меньшей скоростью выезжает мотоцикл. Через некоторое время они встречаются, и в этот момент из В в А выезжает второй мотоцикл, который встречается с автомобилем в точке, отстоящей от точки встречи автомобиля с первым мотоциклом на расстоянии, равном 2/9 пути от А до В. Если бы скорость автомобиля была на 20 км/ч меньше, то расстояние между точками встречи равнялось бы 72 км и первая встреча произошла бы через 3 часа после выезда автомобиля из пункта А. Найти длину пути от А до В (скорости мотоциклов одинаковы). Решение
Ответы к домашнему заданию урока 13 из В.В. Ткачук "Математика - абитуриенту"
- 2,1 м; 3,6 м
- 4 сек; 6 сек
- 45 км
- 7 км/ч
- 6 км/ч; 21 км/ч; 45 км
- 12 мин; 1 час 36 мин
- не успели
- 26/9 мин
- на 48 мин раньше
- 10 час 29 мин
- 390 мин
- 40 км/ч; 30 км/ч
- первая
- не сможет
- 4 часа
- 4 км/ч
- 50 км/ч
- D ниже по течению
- в 4 часа 48 мин
- 40 км/ч; 60 км/ч
- 300 км