Урок 44[2]. Стереометрия. Вспомогательные задачи
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- Докажите, что если двугранные углы трехгранного угла прямые, то его плоские углы тоже прямые.
- Докажите, что трехгранные углы равны, если равны их соответственные двугранные углы.
- Докажите, что сумма двух плоских углов трехгранного угла больше третьего плоского угла.
- Докажите, что сумма двугранных углов трехгранного угла больше
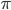 .
. - Луч SC1 лежит внутри трехгранного угла SABC с вершиной S. Докажите, что сумма плоских углов трехгранного угла SABC больше суммы плоских углов трехгранного угла SABC1.
- Пусть
 ,
, 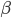 и
и 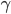 - плоские углы трехгранного угла, а A, B, C - его двугранные углы. Докажите, что имеет место равенство
- плоские углы трехгранного угла, а A, B, C - его двугранные углы. Докажите, что имеет место равенство 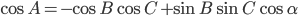 - это утверждение называется второй теоремой косинусов для трехгранного угла.
- это утверждение называется второй теоремой косинусов для трехгранного угла. - Пусть
 ,
, 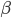 и
и 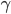 - плоские углы трехгранного угла, а противоположные им ребра образуют с плоскостями граней углы a, b и с. Докажите, что
- плоские углы трехгранного угла, а противоположные им ребра образуют с плоскостями граней углы a, b и с. Докажите, что 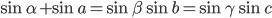 .
. - Докажите, что если все плоские углы трехгранные угла тупые, то все его двугранные углы тоже тупые.
- Докажите, что если все двугранные углы трехгранного угла острые, то и все его плоские углы тоже острые.
- Проведя через каждое ребро тетраэдра плоскость, параллельную противоположному ребру, можно достроить тетраэдр до параллелепипеда. Докажите, что при таком достраивании тетраэдра получается прямоугольный параллелепипед, если и только если все грани тетраэдра есть равные треугольники.
- Две окружности, не лежащие в одной плоскости, пересекаются в двух различных точках А и В. Докажите, что существует единственная сфера, содержащая обе эти окружности.
- Шар радиуса r касается всех ребер треугольной пирамиды. Центр шара лежит внутри пирамиды на ее высоте на расстоянии r
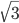 от вершины. Докажите, что пирамида правильная.
от вершины. Докажите, что пирамида правильная. - Шар касается боковых граней треугольной пирамиды в точках пересечения их высот. Докажите, что пирамида правильная.
- Шар касается всех боковых граней треугольной пирамиды в центрах описанных около них окружностей. Известно, кроме того, что все плоские углы при вершине пирамиды равны. Докажите, что пирамида правильная.
- Шар касается всех боковых граней треугольной пирамиды в точках пересечения их медиан. Докажите, что пирамида правильная.
- Шар касается всех боковых граней треугольной пирамиды в точках пересечения их биссектрис. Докажите, что пирамида правильная.
- Дана треугольная пирамида SABC. Шар касается всех сторон треугольника ABC в их серединах и проходит через середины ребер SA, SB и SC. Докажите, что пирамида правильная.
- Докажите, что если все двугранные углы тетраэдра равны, то он правильный.
- Докажите, что объем тетраэдра ABCD равен
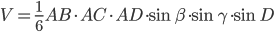 , где
, где 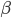 и
и 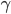 - плоские углы при вершине А, противоположные ребрам АВ и АС, а D - двугранный угол при ребре AD.
- плоские углы при вершине А, противоположные ребрам АВ и АС, а D - двугранный угол при ребре AD. - Площади двух граней тетраэдра равны
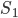 и
и 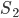 . Известно, что длина их общего ребра равна
. Известно, что длина их общего ребра равна  , а двугранный угол между ними равен
, а двугранный угол между ними равен  . Докажите, что объем тетраэдра равен
. Докажите, что объем тетраэдра равен 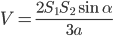 .
.