VI Олимпиада по криптографии и математике
список всех олимпиад по криптографии и математике
Задача 6.1
В системе связи, состоящей из 1997 абонентов, каждый абонент связан ровно с N другими. Определите все возможные значения N.
Задача 6.2
Квадратная таблица размером 1997 × 1997 заполнена натуральными числами от 1 до 1997 так, что в каждой строке присутствуют все числа от 1 до 1997. Найдите сумму чисел, стоящих на диагонали, которая соединяет левый верхний и правый нижний углы таблицы, если заполнение таблицы симметрично относительно этой диагонали.
Задача 6.3
www.itmathrepetitor.ru Текст
А М И М О П Р А С Т Е Т И Р А С И С П Д
И С А Ф Е И И Б О Е Т К Ж Р Г Л Е О Л О
И Ш И С А Н Н С Й С А О О Л Т Л Е Я Т У
И Ц В Ы И П И Я Д П И Щ П Ь П С Е Ю Я Я
получен из исходного сообщения перестановкой его букв. Текст
У Щ Ф М Ш П Д Р Е Ц Ч Е Ш Ю Ш Ч Д А К Е
Ч М Д В К Ш Б Е Е Ч Д Ф Э П Й Щ Г Ш Ф Щ
Ц Е Ю Щ Ф П М Е Ч П М Е Р Щ М Е О Ф Ч Щ
Х Е Ш Р Т Г Д И Ф Р С Я Ы Л К Д Ф Ф Е Е
получен из того же исходного сообщения заменой каждой буквы на другую букву так, что разные буквы заменены разными, а одинаковые - одинаковыми. Восстановите исходное сообщение.
Задача 6.4
На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке 33 зубца, на второй - 10, на третьей - 7.
На каждом зубце первой шестеренки по часовой стрелке написано по одной букве русского языка в алфавитном порядке:
AБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ
На зубцах второй и третьей шестеренки в порядке возрастания по часовой стрелке написаны цифры от 0 до 9 и от 0 до 6 соответственно.
Когда стрелка первой оси указывает на букву, стрелки двух других осей указывают на цифры.
Буквы сообщения шифруются последовательно. Зашифрование производится вращением первой шестеренки против часовой стрелки до первого попадания шифруемой буквы под стрелку. В этот момент последовательно выписываются цифры, на которые указывают вторая и третья стрелки. В начале шифрования стрелка 1-го колеса указывала
на букву А, а стрелки 2-го и 3-го колес - на цифру 0.
а) зашифруйте слово О Л И М П И А Д А;
б) расшифруйте сообщение 2 4 8 0 9 2 8 3 9 1 1 2 1 1.
Задача 6.5
Цифры от 1 до 9 расположены на окружности в некотором неизвестном порядке. При зашифровании цифрового сообщения каждая отличная от 0 цифра заменяется на соседнюю с ней цифру на окружности по часовой стрелке, а при расшифровании - на соседнюю с ней цифру на окружности против часовой стрелки. Цифра 0 остается без изменения в обоих случаях.
Укажите условия, при которых порядок цифр на данной окружности можно однозначно восстановить по двум цифровым текстам - результатам расшифрования и зашифрования одного и того же цифрового текста с помощью данной окружности.
Задача 6.6
Докажите, что для каждого простого числа  последовательность
последовательность 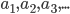 является периодической с периодом 2, если
является периодической с периодом 2, если 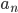 равно остатку от деления числа
равно остатку от деления числа 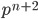 на 24 при всех
на 24 при всех 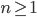 .
.
Задача 6.7
Найдите все значения параметра  , при которых уравнение
, при которых уравнение  имеет ровно 1997 различных решений.
имеет ровно 1997 различных решений.