Вступительный экзамен в ШАД 2013

Условия задач
Вариант 1
- Найдите
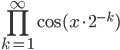
- Дана матрица
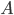 размера
размера  x
x  , где
, где 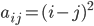 ,
, 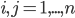 . Найдите ранг матрицы
. Найдите ранг матрицы 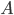 .
. - Имеется множество
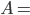 {
{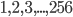 }. Найдите размер максимального по мощности подмножества
}. Найдите размер максимального по мощности подмножества 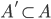 , такого, что
, такого, что 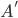 не содержит элементов
не содержит элементов 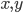 , таких, что
, таких, что 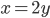 .
. - На окружности случайно выбирается
 точек. Найдите вероятность того, что все они принадлежат некоторой полуокружности.
точек. Найдите вероятность того, что все они принадлежат некоторой полуокружности. - Назовем двумерный массив действительных чисел
![A[1..n][1..n]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_4ceeedf4a017b30cb34e6c5f76f8068a.gif) возрастающим, если для любых
возрастающим, если для любых 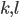
![A[k][l]\ge A[i][j]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_fd3256f0625b85c50526c24f07c819ed.gif) ,
, 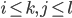 . Задача поиска в квадратном возрастающем массиве формулируется так: для заданного возрастающего массива
. Задача поиска в квадратном возрастающем массиве формулируется так: для заданного возрастающего массива ![A[1..n][1..n]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_4ceeedf4a017b30cb34e6c5f76f8068a.gif) и некоторого числа
и некоторого числа 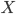 определить, встречается ли число
определить, встречается ли число 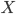 в массиве
в массиве 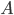 . Покажите, что не существует алгоритма, решающего эту задачу менее чем за
. Покажите, что не существует алгоритма, решающего эту задачу менее чем за  сравнений.
сравнений. - У линейного преобразования
 -мерного пространства существует
-мерного пространства существует 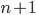 собственных векторов, таких, что любые
собственных векторов, таких, что любые  из них линейно независимы. Найдите всевозможные матрицы, которые могли бы задавать такое преобразование.
из них линейно независимы. Найдите всевозможные матрицы, которые могли бы задавать такое преобразование. - Найдите сумму ряда
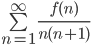 , где
, где 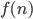 -количество единиц в двоичном представлении числа
-количество единиц в двоичном представлении числа  .
.
Вариант 2
- Последовательность {
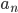 }
}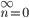 определена рекурсивно
определена рекурсивно 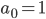 ,
, 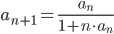 . Найдите формулу общего члена последовательности.
. Найдите формулу общего члена последовательности. - Дано множество
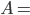 {
{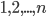 }. Среди всех его подмножеств равновероятно выбирается
}. Среди всех его подмножеств равновероятно выбирается 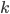 его подмножеств. Найдите вероятность того, что
его подмножеств. Найдите вероятность того, что 
- Дан массив длины
 из нулей и единиц. Найдите в нем подмассив максимальной длины, в котором количество единиц равно количеству нулей. Ограничения:
из нулей и единиц. Найдите в нем подмассив максимальной длины, в котором количество единиц равно количеству нулей. Ограничения: 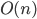 по времени,
по времени, 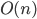 по дополнительной памяти.
по дополнительной памяти. - Пусть
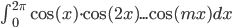 . Для каких
. Для каких ![m\in[1,10]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a921870ab5027ebc3726dfe02e7b0604.gif)
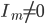 ?
? - Дан неориентированный граф
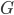 без петель. Пронумеруем все его вершины. Матрица смежности графа
без петель. Пронумеруем все его вершины. Матрица смежности графа 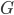 с конечным числом вершин
с конечным числом вершин  (пронумерованных числами от 1 до
(пронумерованных числами от 1 до  ) - это квадратная матрица
) - это квадратная матрица 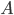 размера
размера  , в которой значение элемента
, в которой значение элемента 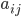 равно числу ребер из
равно числу ребер из 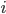 -ой вершины графа в
-ой вершины графа в 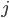 -ю вершину. Докажите, что матрица
-ю вершину. Докажите, что матрица 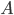 имеет отрицательное собственное значение.
имеет отрицательное собственное значение. - Рассмотрим бесконечный двумерный массив {
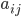 }
}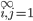 , состоящий из натуральных чисел, причем каждое число встречается в массиве ровно 8 раз. Докажите, что
, состоящий из натуральных чисел, причем каждое число встречается в массиве ровно 8 раз. Докажите, что 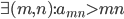 .
. - Дана матрица из нулей и единиц, причем для каждой строки матрицы верно следующее: если в строке есть единицы, то они все идут подряд (неразрывной группой из единиц). Докажите, что определитель такой матрицы может быть равен только
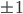 или
или 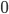 .
.
смотрите еще Вступительные в ШАД 2012 и Контрольная работа от Яндекс, март 2015 г. и Задачи вступительных экзаменов