Вступительный экзамен в ШАД 2015
 2015
2015
Условия задач
- Найдите предел последовательности
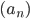 , для которой
, для которой 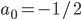 ,
, 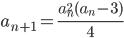
- На плоскости, замощённой одинаковыми прямоугольниками со сторонами 10 и 20 (прямоугольники примыкают сторонами), рисуют случайную окружность радиуса 4. Найдите вероятность того, что окружность имеет общие точки ровно с тремя прямоугольниками.
- Дима и Ваня по очереди заполняют матрицу размера 2n×2n. Цель Вани – сделать так, чтобы получившаяся в итоге матрица имела собственное значение 1, а цель Димы – помешать ему. Дима ходит первым. Есть ли у кого-нибудь из них выигрышная стратегия?
- Найдите определитель матрицы
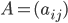 , где
, где 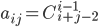 .
. - Даны два массива целых чисел a[1..n] и b[1..k], причём все элементы b различны. Требуется найти набор индексов
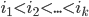 , для которого набор
, для которого набор ![a[i_1],...,a[i_k]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_ac0a7fb070c88e84f8aa95a7b89312f4.gif) является перестановкой элементов массива b, причём разность
является перестановкой элементов массива b, причём разность 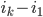 минимально возможная. Ограничение по времени — O(nk) (но, может быть, вы сможете быстрее), по памяти — O(n).
минимально возможная. Ограничение по времени — O(nk) (но, может быть, вы сможете быстрее), по памяти — O(n). - В 2222 году волейбольные турниры проводят по новой системе. Говорят, что команда А превосходит команду В, если А выиграла у В или у какой-либо команды, выигравшей у В. Каждая пара команд играет по одному разу. Ничья исключается волейбольными правилами. Чемпионом объявляют команду, превзошедшую все другие команды. а) Докажите, что чемпион обязательно найдётся; б) Докажите, что не может быть ровно двух чемпионов.
- Вычислите интеграл
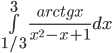
- На плоскости нарисована ломаная с n звеньями. Длина каждого звена равна 1, ориентированный угол между соседними звеньями с равной вероятностью равен α или –α. Найдите математическое ожидание квадрата расстояния от её начальной точки до конечной.
Ответы:
- 0
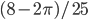
- У Вани
- 1
- -
- -
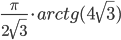
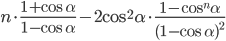
смотрите еще Контрольная работа от Яндекс, март 2015 г. и Задачи вступительных экзаменов