Вступительный экзамен в ШАД 2018

Вступительный экзамен в Школу анализа данных
9 июня 2018
Условия задач
- Пусть
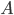 - квадратная матрица
- квадратная матрица  x
x . Докажите, что
. Докажите, что 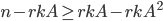
- Сколькими способами
 различных четных чисел и
различных четных чисел и  различных нечетных чисел можно записать в таблицу
различных нечетных чисел можно записать в таблицу 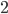 x
x таким образом, чтобы нечетное число никогда не стояло под четным? Ответ должен содержать не более одной суммы.
таким образом, чтобы нечетное число никогда не стояло под четным? Ответ должен содержать не более одной суммы. - На станцию приходят в случайное время две электрички. Времена их приходов независимы и имеют экспоненциальное распределение с плотностью
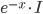 {
{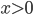 }. Студент приходит на станцию в момент времени 2. Найдите
}. Студент приходит на станцию в момент времени 2. Найдите
a) вероятность того, что он сможет уехать хотя бы на одной электричке;
б) математическое ожидание времени ожидания студентом ближайшей электрички (считаем, что время ожидания равно нулю, если студент опоздал на обе электрички). - Верно ли, что всякая нечетная непрерывная функция, удовлетворяющая условию
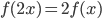 , линейна?
, линейна? - Пусть
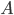 и
и  - ортогональные матрицы (не ортогональные друг другу, а просто ортогональные!). Докажите, что
- ортогональные матрицы (не ортогональные друг другу, а просто ортогональные!). Докажите, что 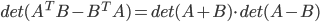 .
. - Назовем элемент прямоугольной матрицы седлом, если он является наибольшим в своей строке и наименьшим в своем столбце или наоборот. Придумайте алгоритм, за
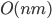 операций находящий все седла в матрице
операций находящий все седла в матрице ![A[1..n][1..m]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_2e6746810c8987feff775ecc279d2075.gif) , использующий не более
, использующий не более 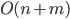 памяти и не более 1 раза обращающийся к каждому элементу
памяти и не более 1 раза обращающийся к каждому элементу 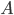 (можете считать, что элемент
(можете считать, что элемент ![A[i][j]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_925242272fe7fc4ce5192a9c0f7f92c3.gif) превращается в
превращается в 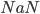 сразу после вызова
сразу после вызова ![A[i][j]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_925242272fe7fc4ce5192a9c0f7f92c3.gif) ). Считайте, что все элементы матрицы различны.
). Считайте, что все элементы матрицы различны. - В компании «Тындекс» работает 100 сотрудников, некоторые из них знакомы друг с другом. Докажите, что найдется такая пара из них, для которой существует хотя бы 50 сотрудников, каждый из которых либо знаком с обоими людьми в этой паре, либо не знаком ни с одним из этой пары.
- Пусть {
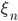 }
}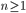 - последовательность случайных величин, имеющих стандартное нормальное распределение. Сходится ли ряд
- последовательность случайных величин, имеющих стандартное нормальное распределение. Сходится ли ряд 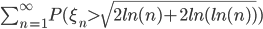 ?
?
смотрите еще Контрольная работа от Яндекс, март 2015 г. и Задачи вступительных экзаменов