Арифметическая и геометрическая прогрессии

Первый уровень

1. Найдите четыре целых числа, из которых первые три составляют арифметическую, а последние три - геометрическую прогрессию, если сумма двух крайних чисел равна 37, а сумма двух средних чисел равна 36.
2. Три числа, первое из которых равно 1, образуют возрастающую геометрическую прогрессию. Если одно из них удвоить, то эти числа, взятые в том же порядке, образуют арифметическую прогрессию. Найдите среднее арифметическое этих трех чисел.
3. Разность между вторым и первым членами геометрической прогрессии равна 4, а разность между ее третьим и вторым членами равна 12. Определите сумму десяти членов арифметической прогрессии, первый и пятый члены которой равны первому и третьему членам геометрической прогрессии.
4. Известно, что существует такая арифметическая прогрессия, в которой первые два члена совпадают с первыми двумя членами геометрической прогрессии, третий на 12 меньше третьего члена геометрической прогрессии, а четвертый член равен 21. Найдите знаменатель геометрической прогрессии.
5. Найдите четыре числа, из которых первые три составляют арифметическую прогрессию, а последние три - геометрическую прогрессию, если сумма двух крайних чисел равна 22, а сумма двух средних чисел равна 20.

Второй уровень

6. Три числа образуют геометрическую прогрессию. Если второе число увеличить на 8, то она станет арифметической. Если после этого увеличить последнее число на 64, то прогрессия снова превратится в геометрическую. Найдите эти числа.
7. Четыре числа составляют геометрическую прогрессию. Если из них вычесть 2, 1, 7 и 27, то вновь полученные числа составят арифметическую прогрессию. Найдите эти числа.
8. Три числа, сумма которых равна 78, образуют геометрическую прогрессию. Их можно рассматривать также как первый, третий и девятый члены арифметической прогрессии. Найдите эти числа.
9. Цифры трехзначного числа составляют геометрическую прогрессию. Если из данного числа вычесть 297, то получится число, написанное теми же цифрами, но в обратном порядке. Если же к цифрам данного числа, начиная с разряда сотен, прибавить соответственно 8,5 и 1, то полученные суммы составят арифметическую прогрессию. Найдите исходное число.
10. Найдите сумму чисел, одновременно являющихся членами арифметической прогрессии 12, 15, 18, ... и геометрической прогрессии 1, 3, 9, ..., если каждая из этих прогрессий содержит по 100 членов.

Ответы

1. 12, 16, 20, 25
2. $5(2+\sqrt{3})/3$
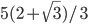
3. 200
4. 3; 5/7
5. 4, 8, 12, 18;  17,5, 12,5, 7,5, 4,5
6. 4, 12, 36; 4/9, -20/9, 100/9
7. 7, 14, 28, 56
8. 6, 18, 54; 26, 26, 26
9. 421
10. 351