- При каких значениях
 оба корня уравнения
оба корня уравнения 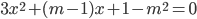 равны нулю?
равны нулю? - Составьте квадратное уравнение с корнями
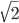 и
и 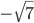 .
. - Не вычисляя корней уравнения
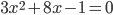 , найдите
, найдите 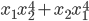 .
. - Пусть
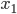 и
и 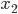 - корни уравнения
- корни уравнения 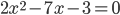 . Составьте квадратное уравнение, корнями которого являются числа
. Составьте квадратное уравнение, корнями которого являются числа 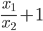 и
и 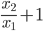 .
. - При каких значениях
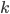 произведение корней уравнения
произведение корней уравнения 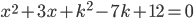 равно нулю?
равно нулю? - При каких значениях
 сумма квадратов корней уравнения
сумма квадратов корней уравнения 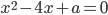 равна 16?
равна 16? - Не вычисляя корней уравнения
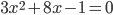 , найдите
, найдите 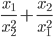 и
и 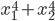 .
. - Составьте квадратное уравнение с корнями
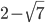 и
и 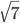 .
. - При каких значениях
 уравнение
уравнение 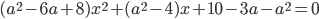 имеет более двух корней?
имеет более двух корней? - Найдите все значения
 , при которых уравнение
, при которых уравнение 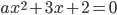 имеет: а) два различных корня; б) не имеет корней.
имеет: а) два различных корня; б) не имеет корней. - Докажите, что уравнение
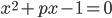 при любом
при любом  имеет два различных корня.
имеет два различных корня. - Докажите, что уравнение
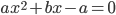 при
при 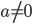 и любом
и любом  имеет два различных корня.
имеет два различных корня. - Корни
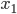 и
и 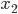 квадратного уравнения
квадратного уравнения 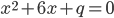 удовлетворяют условию
удовлетворяют условию 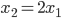 . Найдите
. Найдите 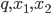
- В уравнении
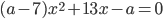 один из корней равен 2. Найдите
один из корней равен 2. Найдите  и второй корень уравнения.
и второй корень уравнения. - Корни квадратного уравнения
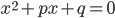 - взаимно обратные положительные числа. Найдите
- взаимно обратные положительные числа. Найдите 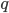
- Сумма квадратов корней уравнения
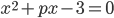 равна 10. Найдите
равна 10. Найдите 
- Найдите
 и
и 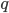 , если числа 10 и -15 являются корнями уравнения
, если числа 10 и -15 являются корнями уравнения 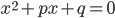
- Запишите квадратное уравнение, корни которого отличались бы от корней уравнения
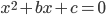 только знаками.
только знаками.
1) 1
2) x*x+(корень(7)-корень(2))x-корень(14)=0
3) 584/81
4) x*x+49x/6-43/6=0
5) 3; 4
6) 0
7) -520/3; 4882/81
8) x*x-2x+2корень(7)-7=0
9) 2