Линейные неравенства
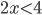
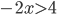
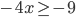
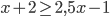
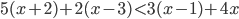
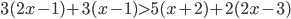
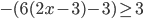
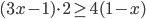
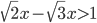
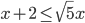
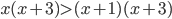
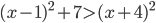
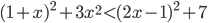
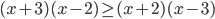
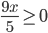
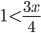
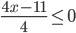
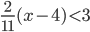
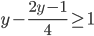
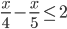
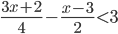
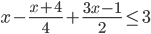
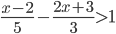
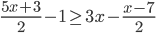
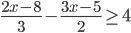
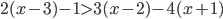
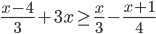
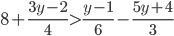
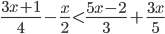
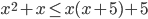
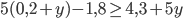
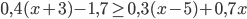
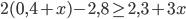
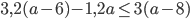
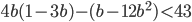
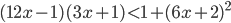
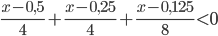
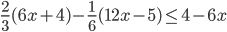
- Найдите наименьшее натуральное число, являющееся решением неравенства
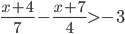
- При каких значениях
 значение дроби
значение дроби 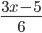 больше значения разности дробей
больше значения разности дробей 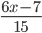 и
и 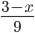 ?
? - При каких
 значение суммы дробей
значение суммы дробей 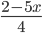 и
и 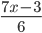 не меньше значения дроби
не меньше значения дроби 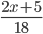 ?
? - При каких натуральных
 разность
разность 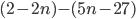 положительна?
положительна?
38) (-беск; 1/16]
40) (-бекс; -3)
41) (-бекс; -10/7]