- Упростите
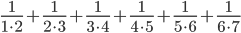 .
. - Найдите значение выражения
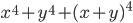 , если
, если 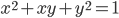 .
. - Найдите
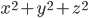 , если
, если 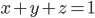 и
и 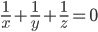 .
. - Найдите
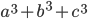 , если
, если 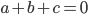 и
и 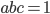 .
. - Найдите значение выражения
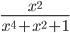 , если
, если 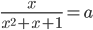
- Докажите, что
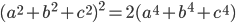 , если
, если 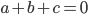 .
. - Про числа
 и
и 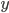 известно, что
известно, что 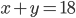 ,
, 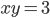 . Вычислите значение выражения
. Вычислите значение выражения 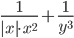
- Сумма десяти чисел равна нулю, и сумма их попарных произведений равна нулю. Чему равна сумма кубов этих чисел?
- Найдите
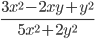 , если
, если 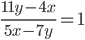
- Вычислите
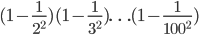
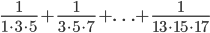
- Вычислите
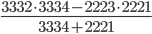
- Попарно различные числа
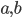 и
и  удовлетворяют равенствам
удовлетворяют равенствам  . Найдите
. Найдите 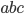
- Упростите
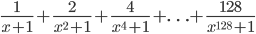
- Известно, что
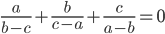 . Найдите
. Найдите 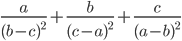
1) 6/7
2) 2
3) 1
4) 3
9) 9/22
10) 101/200
7) 210