Задачи по школьной математике. Треугольник

  1. Две высоты треугольника равны между собой. Дока­жите, что треугольник равнобедренный.

  2. Высоты треугольника ABC, проведенные из вершин B и C, пересекаются в точке M. Известно, что BM = CM. Докажите, что треугольник ABC равнобедренный.

  3. Через вершины A и C треугольника ABC проведены прямые, перпендикулярные биссектрисе угла ABC, пересекаю­щие прямые CB и B A в точках K и M соответственно. Найди­те AB, если BM = 8, KC = 1.

  4. Медиана AM треугольника ABC перпендикулярна его биссектрисе BK. Найдите AB, если BC = 12.

  5. Треугольник ABC – равнобедренный (AB = BC). Отрезок AM делит его на два равнобедренных треугольника с основаниями AB и MC. Найдите угол B.

  6. Равные отрезки AB и CD пересекаются в точке O и делятся ею в отношении AO : OB = CO : OD = 1 : 2. Прямые AD и BC пересекаются в точке M. Докажите, что тре­угольник DMB равнобедренный.

  7. В прямоугольном треугольнике один из углов ра­вен 30◦. Докажите, что в этом треугольнике отрезок перпен­дикуляра,   проведенного  к гипотенузе  через  ее  середину  до пересечения с катетом, втрое меньше большего катета.

  8. Сторона треугольника равна a. Найдите отрезок, со­единяющий середины медиан, проведенных к двум другим сто­ронам.

  9. Две медианы треугольника равны. Докажите, что тре­угольник равнобедренный.

  10. Докажите, что сумма расстояний от произвольной точки внутри равностороннего треугольника до его сторон все­гда одна и та же.

  11. Стороны AB и AC треугольника ABC равны соот­ветственно a и b. На медиане, проведенной к стороне BC, взята точка M. Сумма расстояний от этой точки до прямых AB и AC равна c. Найдите эти расстояния.

  12. Докажите, что площадь прямоугольного треугольни­ка равна произведению отрезков, на которые гипотенуза делит­ся точкой касания со вписанной окружностью.

  13. Точки K и M лежат на сторонах соответственно AB и BC треугольника ABC, причем BK : K A = 1:4, BM : MC = 3:2. Прямая MK пересекает продолжение стороны AC в точке N. Найдите AC : CN.

  14. Точка P лежит на стороне AB треугольника ABC, причем AP : PB = 1:2. Отрезок CP пересекает медиану AD в точке M. Найдите отношения AM : MD, CM : MP.

  15. Точки K и E лежат соответственно на сторонах BC и AB треугольника ABC. Отрезки AK и CE пересекаются в точке M. В каком отношении прямая BM делит сторону AC, если BK : KC = 1 : 2, AE : EB = 2 : 3?
  16. Периметр треугольника ABC равен 8. В треуголь­ник вписана окружность и к ней проведена касательная, парал­лельная стороне AB. Отрезок этой касательной, заключенный между сторонами AC и CB, равен 1. Найдите сторону AB.
  17. Через некоторую точку, взятую внутри треугольника, проведены три прямые, параллельные сторонам. Эти прямые разбивают треугольник на шесть частей, три из которых – треугольники с площадями S1, S2, S3. Найдите площадь данного треугольника.
  18. Высота равнобедренного треугольника больше основания на 2 и меньше боковой стороны на 1. Определите периметр равнобедренного треугольника.
  19. Дан прямоугольный треугольник, у которого один катет больше другого на 5. Если меньший катет этого треугольника уменьшить на 8, а больший увеличить на 4, то получится треугольник, гипотенуза которого равна гипотенузе первого треугольника. Определите периметры треугольников.
  20. Периметр равнобедренного треугольника равен 24. Высота, опущенная на боковую сторону, отсекает от нее отрезок длиной в 2, считая от основания. Определите стороны треугольника.
  21. Найдите площадь треугольника со сторонами 13, 37 и 40.
  22. Стороны треугольника относятся как 7 : 15 : 20, большая высота его равна 24. Найдите стороны треугольника.
  23. В треугольнике АВС медиана АЕ делит высоту BD на отрезки, равные 10/3 и 14/3. Найдите AB и BC, если АС = 21.
  24. Точки F и N делят стороны треугольника АВС в отношении FA:FC = 3:1 и CN:BN = 2:3. Прямые AN и BF пересекаются в точке M. Найдите отношение площадей треугольников AMB и ANB.
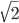
  25. Найдите сторону треугольника, лежащую против угла в 135о, если две другие стороны равны 5 и \(\sqrt{2}\)
  26. Найдите периметр треугольника, длина одной стороны которого равна 4, а прилежащие к ней углы равны 30о и 45о.
  27. Одна из сторон треугольника равна 26, а две другие образуют угол 120о, и их длины относятся как 7:8. Найдите эти стороны.
  28. Найдите площадь треугольника АВС, если ВС = 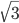\(\sqrt{3}\), АС = 3 и угол АВС равен 60о.
  29. Стороны треугольника равны 5, 7 и 8. Определите вид треугольника и средний по величине угол.
  30. В треугольнике АВС АВ = 3, ВС = 4, АС = 2, BD – высота. Найдите CD.  Ответ: 11/4
  31. В треугольнике АВС АВ = 3, угол САВ равен 30o. Найдите две другие стороны, если их сумма равна 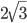\(2\sqrt{3}\). Ответ: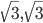 \(\sqrt{3}, \sqrt{3}\)
  32. В треугольнике АВС медианы AD и BE пересекаются в точке О. Определите величину угла А, если АО = ОЕ = АЕ.


Смотрите:

  1. Задачи по школьной математике. Прямоугольный треугольник
  2. Задачи по школьной математике. Высота, медиана и биссектриса треугольника
  3. Задачи по школьной математике. Прямоугольный треугольник 2
  4. Задачи по школьной математике. Углы и их свойства