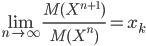Задачи по теории вероятностей. Числовые характеристики дискретных случайных величин

Задачи по теории вероятностей

Числовые характеристики дискретных случайных величин

Содержание

  1. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения: а)
    Х -4 6 10
    р 0,2 0,3 0,5

    б)

    Х 0,21 0,54 0,61
    p 0,1 0,5 0,4
  2. Найти математическое ожидание случайной величины Z, если известны математические ожидания X н Y: а) Z = X-2y, M(X) = 5, M(Y) = 3; б) Z = 3X+4y, M(Х) = 2, M(Y) = 6.
  3. Используя свойства математического ожидания, доказать, что: а) М(Х — Y) = M(X)—М(Y); б) математическое ожидание отклонения X—M(Х) равно нулю.
  4. Дискретная случайная величина X принимает три возможных значения: x1 = 4 с вероятностью р1 = 0,5; х2 = 6 с вероятностью p2 = 0,3 н х3 с вероятностью р3. Найти x3 и p3, зная, что М(Х)=8.
  5. Дан перечень возможных значений дискретной случайной величины X: x1 = —1, х2 = 0, x3 = 1, а также известны математические ожидания этой величины и ее квадрата: M(Х) = 0,1, М(Х2)=0,9. Найти вероятности p1, p2, p3, соответствующие возможным значениям x1, x2, x3.
  6. Дан перечень возможных значений дискретной случайной величины X: x1 = 1, х2 = 2, x3 = 3, а также известны математические ожидания этой величины и ее квадрата: M(Х) = 2,3, М(Х2)=5,9. Найти вероятности p1, p2, p3, соответствующие возможным значениям x1, x2, x3.
  7. В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание дискретной случайной величины X — числа нестандартных деталей среди двух oтобранных.
  8. а) Доказать, что математическое ожидание числа появлений события А в одном испытании равно вероятности р появления события А.б) Доказать, что математическое ожидание дискретной случайной величины X—числа появлений события А в п независимых испытаниях, в каждом из которых вероятность появления события равна р—равно произведению числа испытаний на вероятность появления события в одном испытании, то есть доказать, что математическое ожидание биномиального распределения М(Х) = np.
  9. Найти математическое ожидание дискретной случайной величины X—числа таких бросаний пяти игральных костей, в каждом из которых на двух костях появится по одному очку, если общее число бросаний равно двадцати.
  10. Устройство состоит из n элементов. Вероятность отказа любого элемента за время опыта равна р. Найти математическое ожидание числа таких опытов, в каждом из которых откажет ровно m элементов, если всего произведено N опытов. Предполагается, что опыты независимы один от другого.

  11. Бросают n игральных костей. Найти математическое ожидание числа таких бросаний, в каждом из
    которых выпадет ровно m шестерок, если общее число бросаний равно N.
  12. Бросают n игральных костей. Найти математическое ожидание суммы числа очков, которые выпадут на всех гранях.
  13. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится пять изделий. Найти математическое ожидание дискретной случайной величины X — числа партий, в каждой из которых окажется ровно четыре стандартных изделия,— если проверке подлежит 50 партий.
  14. Доказать: 1) M(Y) = aM(x)+b, если Y=aX+b; 2) M(Y) = a1M(X1)+a2M(X2)+...+anM(Xn)+b, если Y=a1X1+...+anXn+b.
  15. События A1, A2, ..., An несовместны и образуют полную группу; вероятности появления этих событий соответственно равны p1, p2,...,pn. Если в итоге испытания появляется событие Ai (i = 1, 2, ... , n), то дискретная случайная величина X принимает возможное значение хi, равное вероятности pi появления события Ai. Доказать, что математическое ожидание случайной величины X имеет наименьшее значение, если вероятности всех событий одинаковы.
  16. Доказать, что математическое ожидание дискретной случайной величины заключено между наименьшим и наибольшим ее возможными значениями.
  17. Дискретная случайная величина X принимает k положительных значений x1, х2, ..., xk вероятностями, равными соответственно p1,...,pk. Предполагая, что возможные значения записаны в' возрастающем порядке, доказать, что \lim_{n\to\infty}\displaystyle\frac{M(X^{n+1})}{M(X^{n})}=x_k

Содержание



Смотрите:

  1. Задачи по теории вероятностей. Формула Бернулли
  2. Задачи по теории вероятностей. Закон распределения вероятностей дискретной случайной величины. Закон биномиальный и Пуассона
  3. Задачи по теории вероятностей. Простейший поток событий
  4. Задачи по теории вероятностей. Теоретические моменты

Добавить комментарий

Ваш e-mail не будет опубликован. Обязательные поля помечены *