Геометрические вероятности

Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности - вероятности попадания точки в область.
На плоскости задана квадрируемая область, т.е. область, имеющая площадь. Обозначим эту область буквой 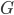 , а ее площадь
, а ее площадь 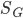 . В области
. В области 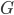 содержится область
содержится область 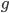 площади
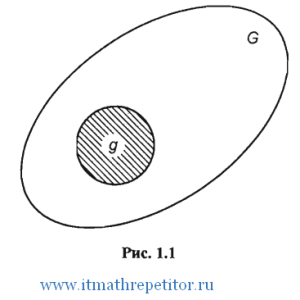
площади 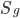 (рис. 1.1). В область
(рис. 1.1). В область 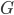 наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области
наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области 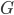 с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть
с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть 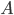 - попадание брошенной точки в область
- попадание брошенной точки в область 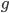 , тогда геометрическая вероятность этого события определяется формулой
, тогда геометрическая вероятность этого события определяется формулой
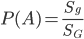 . (1.5.1)
. (1.5.1)
Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема VG, содержащую область g объема Vg:
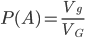 . (1.5.2)
. (1.5.2)
В общем случае понятие геометрической вероятности вводится следующим образом. Обозначим меру области (длину, площадь, объем) через mes g, а меру области G - через mes G (mes - первые три буквы французского слова mesure, что значит мера); обозначим буквой А событие "попадание брошенной точки в области g, которая содержится в области G". Вероятность попадания в область g точки, брошенной в область G, определяется формулой
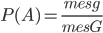 . (1.5.3)
. (1.5.3)
Пример 1. В круг вписан квадрат (рис 1.2). В круг наудачу бросается точка. Какова вероятность того, что точка попадет в квадрат?
Решение.
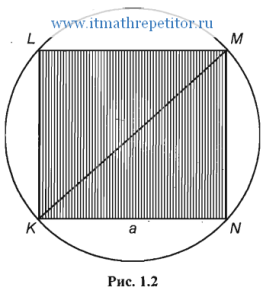
Введем обозначения: R - радиус круга, а - сторона вписанного квадрата, А - попадание точки в квадрат, S - площадь круга, S1 - площадь вписанного квадрата. Как известно, площадь круга 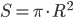 . Сторона вписанного квадрата через радиус описанной окружности выражается формулой
. Сторона вписанного квадрата через радиус описанной окружности выражается формулой 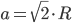 , поэтому площадь квадрата
, поэтому площадь квадрата 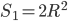 .
.
Полагая в формуле (1.5.1) 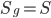 ,
, 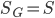 , находим искомую вероятность
, находим искомую вероятность
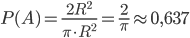 .
.
Пример 2. В квадрат (рис. 1.3) с вершинами в точках O(0, 0), К(0, 1), L(1, 1), М(1, 0) наудачу брошена точка Q(x, у). Найти вероятность того, что координаты этой точки удовлетворяют неравенству 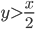 .
.
Решение.
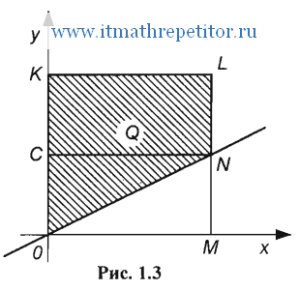
Проведем прямую 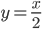 , она пересечет отрезок ML в точке N(1; 1/2). Эта прямая рассекает плоскость на две полуплоскости: для координат точек первой из них (верхней) будет вьmолняться неравенство у > х/2, для второй (нижней) - неравенство у < х/2.
, она пересечет отрезок ML в точке N(1; 1/2). Эта прямая рассекает плоскость на две полуплоскости: для координат точек первой из них (верхней) будет вьmолняться неравенство у > х/2, для второй (нижней) - неравенство у < х/2.
Все точки, принадлежащие квадрату OКLM и координаты которых удовлетворяют неравенству у > х/2, находятся в многоугольнике OКLN. Этот многоугольник состоит из прямоугольника CKLN и треугольника OCN, его площадь S1 =1/2 + 1/4 =3/4. Площадь S квадрата OКLM равна единице: S = 1. В соответствии с формулой (1.5.1), приняв 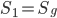 ,
, 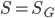 , найдем искомую вероятность
, найдем искомую вероятность
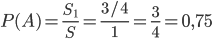 .
.
Пример 3. (Задача Бюффона). Плоскость расчерчена параллельными прямыми, расстояние между которыми равно а. На эту плоскость бросается наудачу отрезок длины l (l < а). Какова вероятность того, что отрезок пересекается хотя бы с одной из прямых семейства?
Решение.
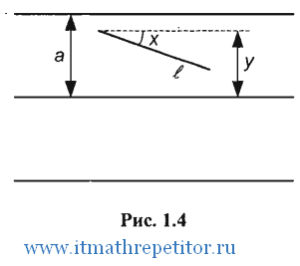
Расстояние от верхнего конца отрезка до ближайшей снизу прямой обозначим через 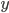 (рис. 1.4). Угол между отрезком и
(рис. 1.4). Угол между отрезком и
лучом, параллельным прямым семейства, начало которого совпадает с верхним концом отрезка, обозначим через  . Очевидно,
. Очевидно, 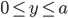 и
и 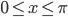 . Для того, чтобы отрезок пересекал хотя бы одну из прямых семейства, необходимо и достаточно, чтобы
. Для того, чтобы отрезок пересекал хотя бы одну из прямых семейства, необходимо и достаточно, чтобы 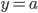 или
или 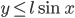 . Выражение "отрезок брошен наудачу" будем понимать так: точка (х,у) наудачу брошена на прямоугольник:
. Выражение "отрезок брошен наудачу" будем понимать так: точка (х,у) наудачу брошена на прямоугольник: 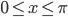 ,
, 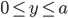 . Точки, координаты которых удовлетворяют неравенству
. Точки, координаты которых удовлетворяют неравенству 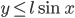 , образуют фигуру, заштрихованную на рис 1.5.
, образуют фигуру, заштрихованную на рис 1.5.
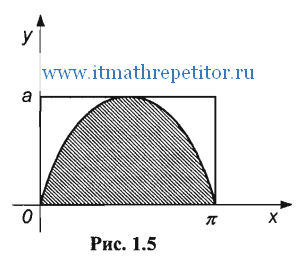
Площадь этой фигуры 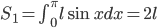 .
.
Площадь всего прямоугольника есть 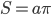 . По формуле (1.5.1), приняв
. По формуле (1.5.1), приняв 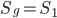 ,
, 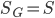 , найдем искомую вероятность
, найдем искомую вероятность 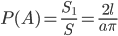 , где А - событие "отрезок пересекается хотя бы с одной прямой".
, где А - событие "отрезок пересекается хотя бы с одной прямой".
Пример 4. В шар вписан куб. Точка наудачу зафиксирована в шаре. Найти вероятность того, что точка попадет в куб.
Решение. Введем обозначения: событие А - "попадание точки в куб"; R - радиус шара, а - ребро куба, V - объем шара, V1 - объем вписанного куба.
Как известно, 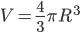 . Поскольку
. Поскольку 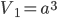 и
и 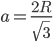 , то
, то 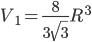 . В соответствии с формулой (1.5.2), приняв
. В соответствии с формулой (1.5.2), приняв 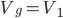 и
и 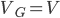 , получим
, получим
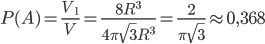 .
.
Задачи
- На плоскости начерчены две концентрические окружности, радиусы которых 6 и 12 см соответственно. Какова вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное указанными окружностями?
- В круг радиуса R вписан правильный треугольник. Найти вероятность того, что точка, брошенная в этот круг, попадет в данный треугольник.
- В квадрат с вершинами O(0, 0), К(0, 1), L(1, 1), М(1, 0) наудачу брошена точка Q(x, у). Какова вероятность того, что координаты этой точки удовлетворяют неравенстау y > 2х?
- В шар вписана правильная треугольная пирамида. Точка наудачу зафиксирована в шаре. Найти вероятность попадания точки в пирамиду.
- Стержень длиной l произвольным образом сломан на три части. Какова вероятность того, что из этих частей можно составить треугольник?
- На плоскости область G ограничена эллипсом
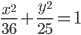 , а область
, а область 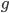 - этим эллипсом и эллипсом
- этим эллипсом и эллипсом 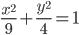 . В область
. В область 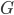 брошена точка. Какова вероятность того, что точка попадет в область
брошена точка. Какова вероятность того, что точка попадет в область 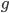 ?
? - В прямоугольник с вершинами К(-2, 0), L(-2, 5), М(1, 5), N(1, 0) брошена точка. Какова вероятность того, что ее координаты (х, у) будут удовлетворять неравенствам
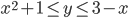 ?
? - В области G, ограниченной эллипсоидом
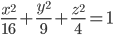 , наудачу зафиксирована точка. Какова вероятность того, что координаты
, наудачу зафиксирована точка. Какова вероятность того, что координаты  ,
, 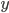 ,
, 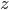 этой точки будут удовлетворять неравенству
этой точки будут удовлетворять неравенству 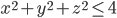 ?
? - В прямоугольник С вершинами R(-2, 0), L(-2,9), М(4, 9), N(4, 0) брошена точка. Найти вероятность того, что ее координаты будут удовлетворять неравенствам
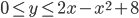 .
. - Область
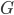 ограничена окружностью
ограничена окружностью 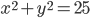 , а область
, а область 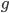 - этой окружностью и параболой
- этой окружностью и параболой 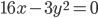 . В область
. В область 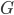 брошена точка. Какова вероятность, что она окажется в области
брошена точка. Какова вероятность, что она окажется в области 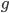 ?
?
Ответы
- 0,75 2.
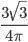 3. 0,25 4.
3. 0,25 4. 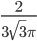 5. 0,25 6. 5/6 7. 0,3 8. 1/3 9. 2/3 10.
5. 0,25 6. 5/6 7. 0,3 8. 1/3 9. 2/3 10. 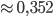
Вопросы
- Как определяется геометрическая вероятность в общем случае?
- Как определяется геометрическая вероятность в пространственном случае?
- Как определяется геометрическая вероятность в плоском случае?
- Как определяется геометрическая вероятность в линейном случае?
- Каковы свойства геометрической вероятности?
- Приведите собственный пример на геометрическую вероятность.