Уравнения и неравенства с модулем
- При
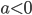 уравнение
уравнение 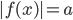 не имеет корней
не имеет корней - При
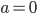 уравнение
уравнение 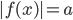 равносильно уравнению
равносильно уравнению 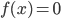 .
. - При
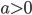 уравнение
уравнение 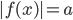 равносильно совокупности
равносильно совокупности 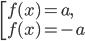
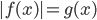

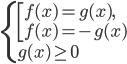
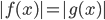

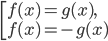
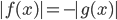

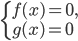
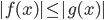

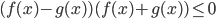
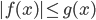

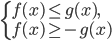
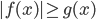

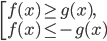
смотрите еще Справочник. Модуль и его свойства
Уравнения и неравенства с модулем
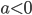 уравнение
уравнение 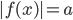 не имеет корней
не имеет корней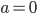 уравнение
уравнение 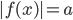 равносильно уравнению
равносильно уравнению 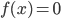 .
.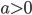 уравнение
уравнение 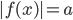 равносильно совокупности
равносильно совокупности 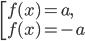
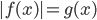

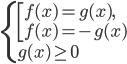
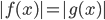

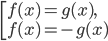
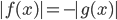

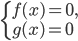
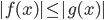

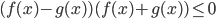
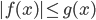

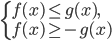
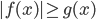

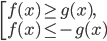
смотрите еще Справочник. Модуль и его свойства