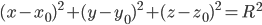Справочник по математике
Метод координат в пространстве
Отрезки
Длина отрезка 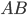 , если
, если 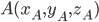 и
и 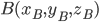
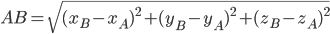
Если т. 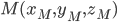 - середина отрезка
- середина отрезка 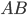 и
и 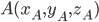 ,
, 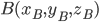 , то
, то 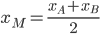 ,
, 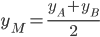 и
и 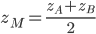
Если т. 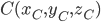 делит отрезок
делит отрезок 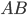 в отношении
в отношении 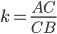 , то
, то
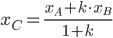 ,
, 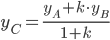 и
и 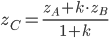
Прямая
Уравнение прямой, проходящей через точки 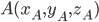 и
и 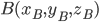
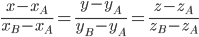
Каноническое уравнение прямой, проходящей через т.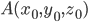 параллельно вектору
параллельно вектору 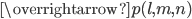
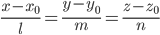
Параметрическое уравнение прямой, проходящей через т.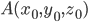 параллельно вектору
параллельно вектору 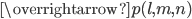
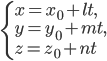
Прямая как пересечение двух плоскостей
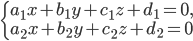
Плоскость
Общее уравнение плоскости
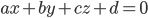 , где
, где 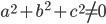
Уравнение плоскости, проходящей через т.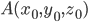 перпендикулярно вектору
перпендикулярно вектору 
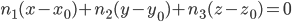
Уравнение плоскости, проходящей через т.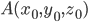 параллельно неколлинеарным векторам
параллельно неколлинеарным векторам 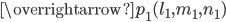 и
и 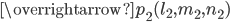
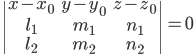
Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой, 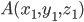 ,
, 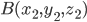 и
и 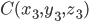
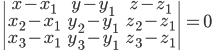
Уравнение плоскости в отрезках
Если 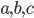 - величины направленных отрезков, отсекаемых плоскостью на осях
- величины направленных отрезков, отсекаемых плоскостью на осях 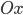 ,
,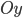 и
и 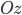 соответственно, то
соответственно, то
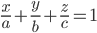
Параметрическое уравнение плоскости, проходящей через т.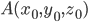 параллельно векторам
параллельно векторам 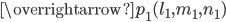 и
и 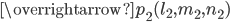
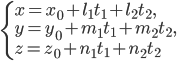
Расстояние 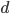 от точки
от точки 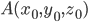 до плоскости
до плоскости 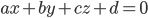
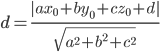
Сфера
Уравнение сферы с центром в точке 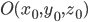 и радиусом
и радиусом