- В угол вписаны две касающиеся внешним образом окружности. Длина большей из них равна
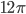 см, расстояние от ее центра до вершины угла равно 30 см. Найдите длину меньшей окружности.
см, расстояние от ее центра до вершины угла равно 30 см. Найдите длину меньшей окружности. - Центральный угол AOC на 18o больше соответствующего вписанного угла ABC. Найдите вписанный угол ABC.
- Около правильного многоугольника описана окружность, и в этот же многоугольник вписана еще одна окружность. Площадь кольца, ограниченного этими окружностями, равна
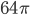 см2. Найдите длину стороны многоугольника.
см2. Найдите длину стороны многоугольника. - Четырехугольник ABCD описан около окружности. Найдите АВ и ВС, если угол АВС = 90o, угол ADC = 60o, AD = 16 см, CD = 30 см.
- Вершины треугольника ABC лежат на окружности, AB : BC = 2 : 3. Точка D делит дугу AC пополам. Отрезок BD пересекает сторону AC в точке E. Через точку E проведена хорда KM, причем KE = 4 см, ME = 6 см. Найдите AC
- Около окружности радиуса
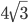 см описан правильный треугольник. На его высоте как на стороне построен правильный шестиугольник, в который вписана другая окружность. Найдите ее радиус.
см описан правильный треугольник. На его высоте как на стороне построен правильный шестиугольник, в который вписана другая окружность. Найдите ее радиус. - Три окружности, радиусы которых 6 см, 2 см и 4 см, касаются друг друга внешним образом. Найдите длину окружности, проходящей через центры данных окружностей.
- В прямоугольной трапеции меньшее основание равно 12 см, радиус вписанной окружности равен 8 см. Найдите площадь трапеции.
- Радиус окружности равен 6 см. Найдите длину хорды, которая стягивает дугу, содержащую 90o
- Через концы диаметра AB к окружности проведены две касательные AM и BN. Третья касательная пересекает первые две в точках C и D так, что С ∈АМ, D ∈ВN. Найдите радиус окружности, если CA=
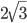 , DB=
, DB=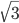 .
. - Центр окружности, описанной около трапеции, лежит на одном из оснований этой трапеции. Найдите площадь трапеции, если ее боковая сторона равна 4 см, а один из ее углов равен 120o
- Длина окружности, описанной около равностороннего треугольника, равна 12π см. Найдите периметр треугольника.
- Найдите длину окружности, вписанной в правильный шестиугольник, если его периметр равен
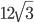 см.
см. - Площадь вписанного в правильный многоугольник круга в 4 раза меньше площади круга, описанного около этого многоугольника. Найдите периметр многоугольника, если его площадь равна
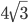 см2
см2 - Хорда окружности равна 24 см, расстояние от центра окружности до прямой, содержащей хорду, равно 5 см. Найдите длину окружности.
- В треугольнике ABC проведена медиана BM, ∠ABC=105°, AC=
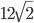 см. Радиус окружности, описанной около треугольника MBC, равен
см. Радиус окружности, описанной около треугольника MBC, равен 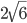 см. Найдите радиус окружности, описанной около треугольника ABM.
см. Найдите радиус окружности, описанной около треугольника ABM. - В окружность радиуса
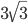 см вписан квадрат. Из одной вершины этого квадрата проведены две хорды, стягивающие дуги по 120o. Найдите длину отрезка диагонали квадрата, заключенного между этими хордами.
см вписан квадрат. Из одной вершины этого квадрата проведены две хорды, стягивающие дуги по 120o. Найдите длину отрезка диагонали квадрата, заключенного между этими хордами. - Вписанный в окружность угол ACB, равный 75o, опирается на дугу AB. Радиус окружности равен 6 см. Найдите площадь треугольника AOB (O — центр окружности).
- Один из углов ромба равен 30o, сторона ромба равна 4 см. Найдите длину окружности, вписанной в ромб.
- В прямоугольном треугольнике один из углов равен 60o, расстояние от центра вписанной окружности до вершины прямого угла равно
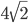 см. Найдите большую сторону этого треугольника
см. Найдите большую сторону этого треугольника - Найдите радиус окружности, описанной около треугольника со сторонами 10 см, 12 см и 10 см.
- В прямоугольную трапецию вписана окружность радиуса 4. Отношение длин оснований трапеции равно 2. Найдите площадь трапеции.
- Найдите радиус окружности, вписанной в равнобедренный треугольник, боковая сторона которого равна 10 см, а основание равно 12 см
- В квадрат со стороной, равной 8 см, вписана окружность. Найдите площадь круга, ограниченного этой окружностью.
- Дана окружность, длина которой равна 12π. Найдите площадь сектора круга, ограниченного этой окружностью, если угол этого сектора равен 40°.
- В треугольнике ABC проведена высота BH. Биссектриса угла A делит высоту BH в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=12.
- В равнобедренном треугольнике ABC известно, что AB=BC=4, медиана AM=3. Найдите площадь круга с диаметром AC.
- Дан прямоугольный треугольник, один из катетов которого равен 6 см, а радиус окружности, описанной около этого треугольника, равен 5 см. Найдите радиус окружности, вписанной в этот треугольник
- Найдите площадь равнобедренной трапеции, в которую вписана окружность и точка касания делит боковую сторону на отрезки, равные 4 см и 9 см.
- В окружности длиной 18π см проведена хорда, равная 9 см. Найдите длину меньшей дуги, стягиваемой этой хордой.
- В угол A вписана окружность с центром в точке O, которая касается сторон угла в точках B и C. Найдите угол BCO, если ∠A =64o
- Прямоугольная трапеция описана около окружности. Точка касания делит большую боковую сторону на отрезки, равные 2 см и 8 см. Найдите площадь трапеции.
Ответы

- 18o
- 16
- 10;24
- 10
- 18
- 5
- 288
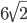
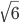
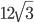


- 12

- 6
- 6
- 9
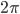

- 6,25
- 72
- 3

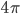
- 7,5
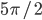
- 2
- 156

- 32o
- 72