ЕГЭ 2014 Типовой вариант 1
Условия задач с ответами и решениями
B1. Теплоход рассчитан на 600 пассажиров и 20 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
B2. При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси - напряжение в вольтах. Определите по рисунку, какое напряжение будет в цепи через 15 часов работы фонарика. Ответ дайте в вольтах.

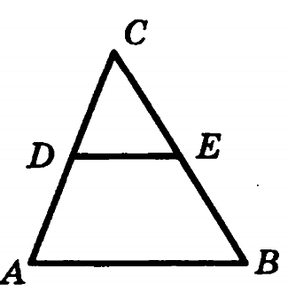
B3. В треугольнике ABC DE - средняя линия. Площадь треугольника CDE равна 24. Найдите площадь треугольника ABC.
B4. Телефонная компания предоставляет на выбор три тарифных плана.
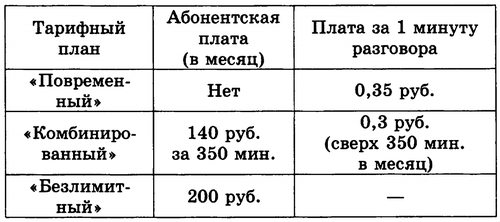
Абонент выбрал самый дешевый тарифный план исходя из предположения, что общая длительность телефонных разговоров составляет 700 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 700 минутам? Ответ дайте в рублях.
B5. Найдите корень уравнения 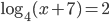
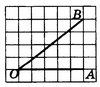
B6. Найдите тангенс угла АОВ, изображенного на клетчатой бумаге.
B7. Найдите значение выражения 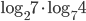 .
.
B8. На рисунке изображен график 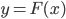 одной из первообразных некоторой функции
одной из первообразных некоторой функции 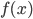 , определенной на интервале (-7; 5). Пользуясь рисунком, определите количество решений уравнения
, определенной на интервале (-7; 5). Пользуясь рисунком, определите количество решений уравнения 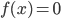 на отрезке [-5; 2].
на отрезке [-5; 2].

B9. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1 = 16, A1B1 = 2, A1D1 = 8. Найдите длину диагонали.

B10. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.
B11. В сосуде, имеющем форму конуса, уровень жидкости достигает 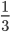 высоты. Объем жидкости равен 12 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
высоты. Объем жидкости равен 12 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

B12. Зависимость объема спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задается формулой 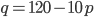 . Выручка предприятия за месяц r (тыс. руб.) вычисляется по формуле
. Выручка предприятия за месяц r (тыс. руб.) вычисляется по формуле 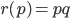 . Определите наибольшую цену p, при которой месячная выручка r(p) составит 320 тыс. руб. Ответ приведите в тыс. руб.
. Определите наибольшую цену p, при которой месячная выручка r(p) составит 320 тыс. руб. Ответ приведите в тыс. руб.
B13. В сосуд, содержащий 7 литров 15-процентного водного раствора некоторого вещества, добавили 8 литров воды. Сколько процентов составит концентрация получившегося раствора?
B14. Найдите наибольшее значение функции 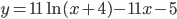 на отрезке
на отрезке ![[-3,5; 0]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_51a201ec3b0530268249c9af9f616295.gif)
С1. а) Решите уравнение 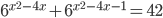 ; б) Найдите все корни этого уравнения, принадлежащие отрезку
; б) Найдите все корни этого уравнения, принадлежащие отрезку ![[-2; 4]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_61be2a2141ba27aca9bd9553016be962.gif) .
.
С2. В правильной треугольной пирамиде SABC с вершиной S, все ребра которой равны 6, точка М - середина ребра BC, точка О - центр основания пирамиды, точка F делит отрезок SO в отношении 1:2, считая от вершины пирамиды. Найдите угол между плоскостью MCF и плоскостью АВС.
С3. Решите систему неравенств 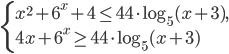
С4. Окружность, построенная на стороне AD параллелограмма ABCD как на диаметре, проходит через точку пересечения диагоналей параллелограмма. а) Докажите, что ABCD - ромб. б) Эта окружность пересекает сторону АВ в точке М, причем АМ : МВ = 1 : 2. Найдите диагональ АС, если известно, что AD = 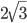
С5. Найдите все значения параметра 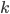 , при каждом из которых уравнение
, при каждом из которых уравнение 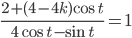 не имеет решений на интервале
не имеет решений на интервале 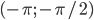 .
.
С6. Найдите наименьшее и наибольшее натуральные значения  , при которых уравнение
, при которых уравнение 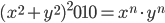 имеет натуральные решения.
имеет натуральные решения.
Ответы
B1. 9
B2. 0,8
B3. 96
B4. 200
B5. 9
B6. 0,8
B7. 2
B8. 3
B9. 18
B10. 0,5
B11. 312
B12. 8
B13. 7
B14. 28
C1. а)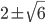 ; б)
; б) 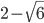
C2. 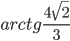
C3. 2
C4. 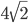
C5. 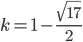 или
или 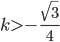
C6. 2011, 3015