Подготовка к ЕГЭ. Наибольшее и наименьшее значения функции
- Найдите стационарные точки функции
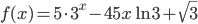
- Найдите значение функции
![y=2x^3-3x^2(\sqrt[4]{x-3})^4+21x](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_9dc0ed71c24ef124c599430d57a36283.gif) в точке максимума
в точке максимума - Найдите значение функции
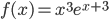 в точках экстремума
в точках экстремума - Найдите точки экстремума функции
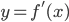 , если
, если 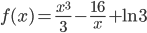
- Найдите целые точки экстремума функции
![y=(x-2)^3(x-3)^2+\sqrt[3]{7}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_32c9d9c79bb5253ae7556faefb2accc5.gif)
- Найдите наименьшее значение функции
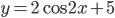 на промежутке
на промежутке ![[\pi/3; \pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_ebefddbcbeb0d310f2c6a863cc87349b.gif)
- Найдите разность наибольшего и наименьшего значений функции
![y=4\sqrt[3]{x}-\sqrt[3]{x^4}+3\ln 2](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_50c4ee935c00b78836fe1de8181274f4.gif) на отрезке [0; 1]
на отрезке [0; 1] - Найдите наибольшее значение функции
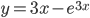 на отрезке [-1; 1]
на отрезке [-1; 1] - Найдите экстремумы функции
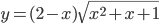
- Найдите значения функции
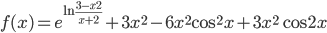 в точках максимума
в точках максимума - Найдите точки минимума функции
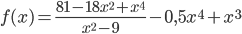
- Найдите точки экстремума функции
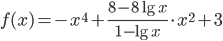
- Найдите наибольшее и наименьшее значения функции
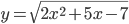 на отрезке [4;5]
на отрезке [4;5] - Найдите наименьшее значение функции
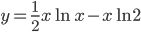 среди ее в точках минимума
среди ее в точках минимума - Найдите наибольшее и наименьшее значения функции
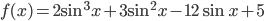 на отрезке
на отрезке ![[-\pi/2; \pi/2]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_847739c7f4745ec9262b1ac20becd125.gif)
- Найдите значение функции
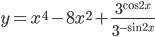 в точке максимума
в точке максимума
Ответы
- 2
- 245
- -27
- -2; 2
- 3
- 3
- 3
- -1
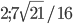
- 2
- 0
- 2
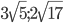
- -2/e
- 18; -2
- 3