Справочник олимпиадника. Четырехугольник

к содержанию справочника

1. Сумма диагоналей выпуклого четырёхугольника больше суммы его двух противоположных сторон.

2. Если отрезки, соединяющие середины противоположных сторон  четырёхугольника

       а) равны, то диагонали четырёхугольника перпендикулярны;

       б) перпендикулярны, то диагонали четырёхугольника равны.

3. Биссектрисы углов при боковой стороне трапеции пересекаются на её средней линии.

4. Стороны параллелограмма равны $a$ и $b$. Тогда четырёхугольник, образованный пересечениями биссектрис углов паралле­лограмма, является прямоугольником, диагонали которого равны $|a-b|$.

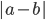5. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований трапеции, равен их полуразности.

6. На сторонах АВ и AD параллелограмма ABCD взяты точки М и N так, что прямые МС и NC делят параллелограмм на три равновеликие части. Найдите MN, если BD=d.

7. Отрезок прямой, параллельной основаниям трапеции, заключённый внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой.

8. Через точку пересечения диагоналей трапеции с основаниями $a$ и $b$проведена прямая, параллельная основаниям. Отрезок этой прямой, заключенный между боковыми сторонами трапеции, равен $\displaystyle\frac{2ab}{a+b}$ .

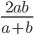9. Трапеция разделена прямой, параллельной её основаниям, равным $a$ и $b$, на две равновеликие трапеции. Тогда отрезок этой прямой, заключённый между боковыми сторонами, равен  $\sqrt{\frac{a^2+b^2}{2}}$ .

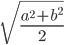10. Если выполняется одно из следующих условий, то четыре точки А, В, С и D лежат на одной окружности.

       а) CAD=CBD = 90°.

       б) точки А и В лежат по одну сторону от прямой CD и угол CAD равен углу CBD.

       в) прямые АС и BD пересекаются в точке О и О А•ОС=ОВ•OD.

11. Прямая, соединяющая точку Р пересечения диагоналей четырехугольника ABCD с точкой Q пересечения прямых АВ и CD, делит сторону AD пополам. Тогда она делит пополам и сторону ВС.

12. Каждая сторона выпуклого четырёхугольника поделена на три равные части. Соответствующие точки деления на противоположных сторонах соединены отрезками. Тогда эти отрезки делят друг друга на три равные части.

13. Две прямые делят каждую из двух противоположных сторон выпуклого четырёхугольника на три равные части. Тогда между этими прямыми заключена треть площади четырёхугольника.

14. Если в четырёхугольник можно вписать окружность, то отрезок, соединяющий точки, в которых вписанная окружность касается противоположных сторон четырёхугольника, проходит через точку пересечения диагоналей.

15. Если суммы противоположных сторон четырёхугольника равны, то в такой четырёхугольник можно вписать окружность.

16. Свойства вписанного четырёхугольника со взаимно перпендикулярными диагоналями. Четырёхугольник ABCD вписан в окружность радиуса R. Его диагонали АС и BD взаимно перпендикулярны и пересекаются в точке Р. Тогда

       а) медиана треугольника АРВ перпендикулярна стороне CD;

       б) ломаная АОС делит четырёхугольник ABCD на две равновеликие фигуры;

       в) АВ²+CD²=4R²;

       г) АР²+ВР²+СР²+DP²=4R² и АВ²+ВС²+CD²+AD²=8R²;

       д) расстояние от центра окружности до стороны четырёхугольника вдвое меньше противоположной стороны.

       е) если перпендикуляры, опущенные на сторону AD из вершин В и С, пересекают диагонали АС и BD в точках Е и F, то BCFE — ромб;

      ж) четырёхугольник, вершины которого — проекции точки Р на стороны четырёхугольника ABCD, — и вписанный, и описанный;

      з) четырёхугольник, образованный касательными к описанной окружности четырёхугольника ABCD, проведёнными в его вершинах, можно вписать в окружность.

17. Если a, b, c, d — последовательные стороны четырёхугольника, S — его площадь, то 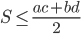$S\le\frac{ac+bd}{2}$, причем равенство имеет место только для вписанного четырёхугольника, диагонали которого взаимно перпендикулярны.

18. Формула Брахмагупты. Если стороны вписанного четырехугольника равны a, b, с и d, то его площадь S может быть вычислена по формуле 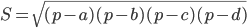$S=\sqrt{(p-a)(p-b)(p-c)(p-d)}$,

где 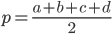$p=\frac{a+b+c+d}{2}$ — полупериметр четырехугольника.

19. Если четырёхугольник со сторонами а, b, с, d можно вписать и около него можно описать окружность, то его площадь равна 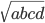$\sqrt{abcd}$.

20. Точка Р расположена внутри квадрата ABCD, причем угол PAB равен углу РВА и равен 15°. Тогда треугольник DPC — равносторонний.

21. Если для вписанного четырёхугольника ABCD выполнено равенство CD=AD+ВС, то биссектрисы его углов А и В пересекаются на стороне CD.

22. Продолжения противоположных сторон АВ и CD вписанного четырёхугольника ABCD пересекаются в точке М, а сторон AD и ВС — в точке N. Тогда

а) биссектрисы углов AMD и DNC взаимно перпендикулярны;

б) прямые МQ и NQ пересекают стороны четырёхугольника в вер­шинах ромба;

в) точка пересечения Q этих биссектрис лежит на отрезке, соеди­няющем середины диагоналей четырёхугольника ABCD.

23. Теорема Птолемея. Сумма произведений двух пар противопо­ложных сторон вписанного четырёхугольника равна произведению его диагоналей.

24. Теорема Ньютона. Во всяком описанном четырёхугольнике середины диагоналей и центр вписанной окружности расположены на одной прямой.

25. Теорема Монжа. Прямые, проведённые через середины сторон вписанного четырёхугольника перпендикулярно противоположным сторонам, пересекаются в одной точке.

27. Четыре круга, построенных на сторонах выпуклого четырёхугольника как на диаметрах, покрывают весь четырёхугольник.

29. Два противоположных угла выпуклого четырёхугольника — тупые. Тогда  диагональ, соединяющая вершины этих углов, меньше другой диагонали.

30. Центры квадратов, построенных на сторонах параллелограмма вне его, сами образуют квадрат.