Решебник домашнего задания урока 1
В.В. Ткачук "Математика - абитуриенту"
Задачи 1 - 5

Приступим к разбору домашнего задания первого урока. Сразу замечу, что задачи идут не по возрастанию сложности (и не по убыванию). А сам принцип, по которому определялся порядок задач в списке, я не смог определить. Если есть догадки, поделитесь.
1. К слагаемому  применим формулу двойного угла (формула 17 в справочнике). Тогда
применим формулу двойного угла (формула 17 в справочнике). Тогда 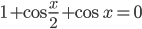
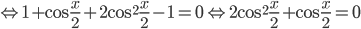
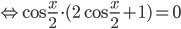 . Значит,
. Значит, 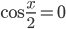 или
или 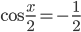 . Откуда
. Откуда 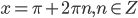 или
или 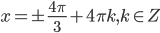 .
.
2. К слагаемому  применим формулу двойного аргумента (формула 18 в справочнике). Тогда
применим формулу двойного аргумента (формула 18 в справочнике). Тогда 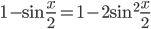
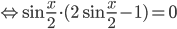 . Откуда,
. Откуда, 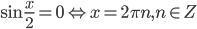 или
или 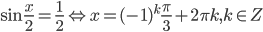 .
.
3. К слагаемому 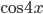 применим формулу двойного аргумента (формула 17). Уравнение принимает вид
применим формулу двойного аргумента (формула 17). Уравнение принимает вид 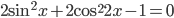 . Далее к слагаемому
. Далее к слагаемому 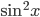 применим формулу понижения степени (формула 25). Тогда
применим формулу понижения степени (формула 25). Тогда 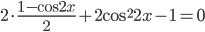 . После проведения подобных слагаемых и разложения на множители левой части уравнения приходим к совокупности уравнений
. После проведения подобных слагаемых и разложения на множители левой части уравнения приходим к совокупности уравнений 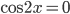 и
и 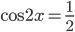 . Откуда
. Откуда 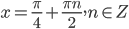 или
или 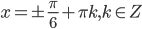 .
.
4. К слагаемому 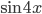 применим формулу двойного аргумента (формула 15), а выражение
применим формулу двойного аргумента (формула 15), а выражение 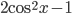 свернем по формуле двойного аргумента для косинуса (формула 17). Тогда
свернем по формуле двойного аргумента для косинуса (формула 17). Тогда 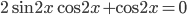 . Откуда
. Откуда 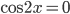 или
или 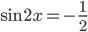 , то есть
, то есть 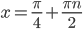 или
или 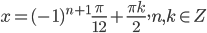 .
.
И последняя задача в этом посте.
5. Заменим 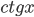 на
на 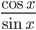 и приведем левую часть к общему знаменателю. Получим уравнение
и приведем левую часть к общему знаменателю. Получим уравнение 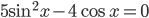 , при этом не забудем, что
, при этом не забудем, что 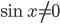 , иначе котангенс не существует. Далее с помощью основного тригонометрического тождества (формула 1 в справочнике) от
, иначе котангенс не существует. Далее с помощью основного тригонометрического тождества (формула 1 в справочнике) от 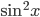 переходим к
переходим к 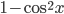 и после замены
и после замены 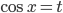 приходим к квадратному уравнению
приходим к квадратному уравнению 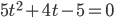 , корнями которого являются числа
, корнями которого являются числа 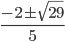 . Так как значения косинуса по модулю не могут быть более единицы, то уравнение
. Так как значения косинуса по модулю не могут быть более единицы, то уравнение 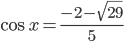 корней не имеет. Во втором уравнении
корней не имеет. Во втором уравнении 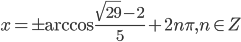 .
.
Ссылки на следующие посты с решениями будут появляться здесь. Спасибо за внимание.
Легкие можно не рассказывать))
думаю, пригодятся
Насчет дз - закономерности в приниципе и не должно быть никакой. Все подряд, чтобы не привыкатть к метоадам