Варианты вступительных экзаменов в МФТИ 2008 г. по математике
Вариант 1
- Решите неравенство
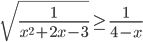 .
. - Решите уравнение
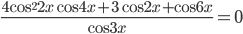 .
. - Найдите действительные решения системы уравнений
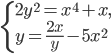
- Параллелограмм ABCD имеет площадь 4. Окружность с центром в точке О, расположенной на отрезке AD, касается отрезков AB, BC и прямой CD в точках M, N и K соответственно. Найти радиус этой окружности и стороны параллелограмма ABCD, если CK:BM=3:1.
- Найти все пары действительных чисел
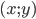 , удовлетворяющие неравенству
, удовлетворяющие неравенству 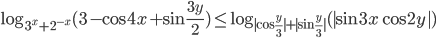 .
. - На основании ABCD четырехугольной пирамиды SABCD расположена точка O. Сфера с центром в точке О касается прямых SA, SB, SC, SD в точках A, B, K, L соответственно. Известно, что AB = KL =
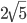 , AL = 2, BK = 6, а отрезок SO составляет с плоскостью ABCD угол arccos
, AL = 2, BK = 6, а отрезок SO составляет с плоскостью ABCD угол arccos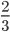 . Найти длины отрезков AK, OS и SD.
. Найти длины отрезков AK, OS и SD.
Вариант 5
- Решите неравенство
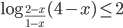 .
. - Решите уравнение
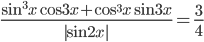 .
. - Решите систему уравнений
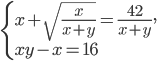
- В треугольнике ABC медиана BM равна 2, угол ABM равен
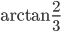 , угол CBM равен
, угол CBM равен 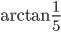 . Найти стороны AB, BC и биссектрису BE треугольника ABC.
. Найти стороны AB, BC и биссектрису BE треугольника ABC. - Решите систему уравнений
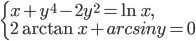
- В основании пирамиды SABCD лежит параллелограмм ABCD. Сфера
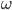 радиуса
радиуса 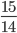 с центром O касается ребер AS, BS, AD, BC пирамиды SABCD соответственно в точках K, L, M, N, пересекает ребро AB в точках P и Q и касается грани CDS. Известно, что прямая SO перпендикулярна плоскости ABCD и пересекает ее в точке H, AB:PQ = 4:
с центром O касается ребер AS, BS, AD, BC пирамиды SABCD соответственно в точках K, L, M, N, пересекает ребро AB в точках P и Q и касается грани CDS. Известно, что прямая SO перпендикулярна плоскости ABCD и пересекает ее в точке H, AB:PQ = 4: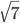 , AS:LS=3:2. Найти угол SAB, угол SBH, высоту пирамиды и ее объем.
, AS:LS=3:2. Найти угол SAB, угол SBH, высоту пирамиды и ее объем.
Ответы:
Вариант 1
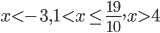
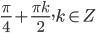
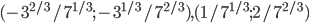
![R=\sqrt[4]{3},AB=2/\sqrt[4]{3},AD=4/\sqrt[4]{3}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_7115f99dd4e1ef69aaa4de6b780ebda9.gif)
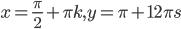 или
или 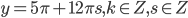
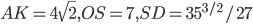
Вариант 5
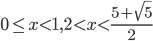
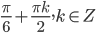
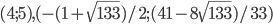
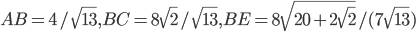
- (1;-1)
- arccos(4/9), arccos(5/9), h=2, V=64/21