§ 9. Уравнения с модулем

Задачи 3.291 - 3.320 с ответами

Содержание задачника

Решите уравнение:

3.291 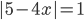$\displaystyle |5-4x|=1$
3.292 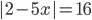$\displaystyle |2-5x|=16$
3.293 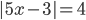$\displaystyle |5x-3|=4$ 
3.294 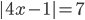$\displaystyle |4x-1|=7$
3.295 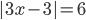$\displaystyle |3x-3|=6$
3.296 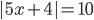$\displaystyle |5x+4|=10$  
3.297 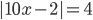$\displaystyle |10x-2|=4$  
3.298 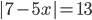$\displaystyle |7-5x|=13$  
3.299 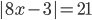$\displaystyle |8x-3|=21$  
3.300 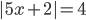$\displaystyle |5x+2|=4$  

Найдите целочисленные решения уравнения:

3.301 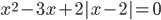$\displaystyle x^2-3x+2|x-2|=0$  
3.302 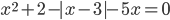$\displaystyle x^2+2-|x-3|-5x=0$  
3.303 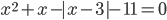$\displaystyle x^2+x-|x-3|-11=0$  
3.304 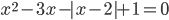$\displaystyle x^2-3x-|x-2|+1=0$  
3.305 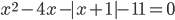$\displaystyle x^2-4x-|x+1|-11=0$  
3.306 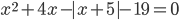$\displaystyle x^2+4x-|x+5|-19=0$  
3.307 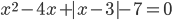$\displaystyle x^2-4x+|x-3|-7=0$  
3.308 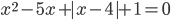$\displaystyle x^2-5x+|x-4|+1=0$  
3.309 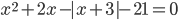$\displaystyle x^2+2x-|x+3|-21=0$  
3.310 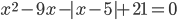$\displaystyle x^2-9x-|x-5|+21=0$  

Решите уравнение:

3.311 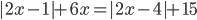$\displaystyle |2x-1|+6x=|2x-4|+15$  
3.312 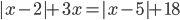$\displaystyle |x-2|+3x=|x-5|+18$  
3.313 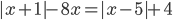$\displaystyle |x+1|-8x=|x-5|+4$  
3.314 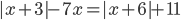$\displaystyle |x+3|-7x=|x+6|+11$  
3.315 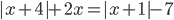$\displaystyle |x+4|+2x=|x+1|-7$  
3.316 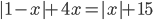$\displaystyle |1-x|+4x=|x|+15$  
3.317 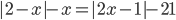$\displaystyle |2-x|-x=|2x-1|-21$  
3.318 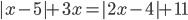$\displaystyle |x-5|+3x=|2x-4|+11$  
3.319 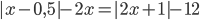$\displaystyle |x-0,5|-2x=|2x+1|-12$  
3.320 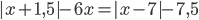$\displaystyle |x+1,5|-6x=|x-7|-7,5$  

Ответы

3.291  1; 1,5
3.292  -2,8; 3,6
3.293  -0,2; 1,4
3.294  -1,5; 2
3.295  -1; 3
3.296  -2,8; 1,2
3.297  -0,2; 0,6
3.298  -1,2; 4
3.299  -2,25; 3
3.300  -1,2; 0,4
3.301  1
3.302  5
3.303  -4
3.304  3
3.305  -2
3.306  -7
3.307  5
3.308  1
3.309  -6
3.310  4
3.311  2
3.312  5
3.313  -1,25
3.314  -2
3.315  -3
3.316  4
3.317  10
3.318  6
3.319  3,5
3.320  0,5