Сканави М.И.
Задачи по планиметрии с ответами и решениями

перейти к содержанию

Группа А. Задачи 101 - 150 (с ответами и решениями)

101. В прямоугольный треугольник с катетами а и b  вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата. Ответ: 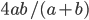$4ab/(a+b)$  Решение

102. В правильный треугольник вписан квадрат, сторона которого равна m. Найти сторону треугольника. Ответ: 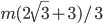$m(2\sqrt{3}+3)/3$  Решение

103. Найти площадь квадрата, вписанного в правильный треугольник со стороной а. Ответ: 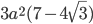 $3a^2(7-4\sqrt{3})$ Решение

104. Сторона правильного треугольника, вписанного в окружность, равна а. Вычислить площадь квадрата, вписанного в ту же окружность. Ответ: 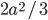 $2a^2/3$ Решение

105. На сторонах квадрата вне его построены правильные треугольники, и их вершины последовательно соединены. Определить отношение периметра полученного четырехугольника к периметру данного квадрата. Ответ: 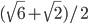$(\sqrt{6}+\sqrt{2})/2$  Решение

106. В квадрате, сторона которого а, середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Найти площадь полученного треугольника. Ответ: 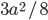$3a^2/8$  Решение

107. В равнобедренный треугольник вписан квадрат единичной площади, одна сторона которого лежит на основании треугольника. Найти площадь треугольника, если известно, что центры масс треугольника и квадрата совпадают (центр масс треугольника лежит на пересечении его медиан). Ответ:  9/4 Решение

108. Площадь равнобедренного треугольника равна 1/3 площади квадрата, построенного на основании данного треугольника. Длины боковых сторон треугольника короче длины его основания на 1 см. Найти длины сторон и высоты треугольника, проведенной к основанию. Ответ: 4; 6  Решение
109. Найти площадь правильного треугольника, вписанного в квадрат со стороной а при условии, что одна из вершин треугольника совпадает с вершиной квадрата. Ответ: 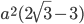$a^2(2\sqrt{3}-3)$  Решение
110. На сторонах равнобедренного прямоугольного треугольника с гипотенузой с вне этого треугольника построены квадраты. Центры этих квадратов соединены между собой. Найти площадь полученного треугольника. Ответ: 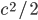$c^2/2$  Решение
111. В квадрате со стороной а середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Определить площадь внутреннего треугольника. Ответ: 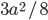$3a^2/8$  Решение
112. В квадрат вписан другой квадрат, вершины которого лежат на сторонах первого, а стороны составляют со сторонами первого квадрата углы в 60°. Какую часть площади данного квадрата составляет площадь вписанного? Ответ: 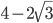$4-2\sqrt{3}$  Решение
113. Дан квадрат, две вершины которого лежат на окружности радиуса R, две другие — на касательной к этой окружности. Найти длину диагонали квадрата. Ответ: 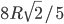$8R\sqrt{2}/5$  Решение
114. Около квадрата со стороной а описана окружность. В один из образовавшихся сегментов вписан квадрат. Определить площадь этого квадрата. Ответ: 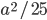$a^2/25$  Решение
115. В сегмент, дуга которого равна 60°, вписан квадрат. Вычислить площадь квадрата, если радиус круга равен 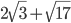$2\sqrt{3}+\sqrt{17}$. Ответ: 1  Решение
116. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого равна 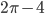$2\pi-4$ см². Найти площадь квадрата. Ответ: 16  Решение
117. Площадь прямоугольника равна 9 см², а величина одного из углов, образованного диагоналями, равна 120°. Найти стороны прямоугольника. Ответ:  $3\sqrt[4]{3}; \sqrt[4]{27}$ Решение
118. В круг радиуса R вписан прямоугольник, площадь которого вдвое меньше площади круга. Определить стороны прямоугольника. Ответ: 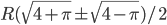$R(\sqrt{4+\pi}\pm\sqrt{4-\pi})/2$  Решение
119. В прямоугольнике проведены биссектрисы двух углов, прилежащих к большей стороне. Определить, на какие части делится площадь прямоугольника этими биссектрисами, если стороны прямоугольника равны 2 и 4 м. Ответ: 2,2; 4  Решение
120. В прямоугольный треугольник с углом 60° вписан ромб со стороной, равной 6 см, так, что угол в 60° у них общий и все вершины ромба лежат на сторонах треугольника. Найти стороны треугольника. Ответ: 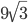$9\sqrt{3}$  Решение
121. В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 2 : 3. Диагонали ромба равны n и m. Найти стороны треугольника, содержащие стороны ромба. Ответ: 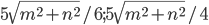$5\sqrt{m^2+n^2}/6; 5\sqrt{m^2+n^2}/4$  Решение
122. Сумма длин диагоналей ромба равна m, а его площадь равна S. Найти сторону ромба. Ответ: 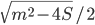$\sqrt{m^2-4S}/2$  Решение
123. В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найти площадь ромба. Ответ: 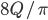$8Q/\pi$  Решение
124. Периметр ромба равен 2 м, длины его диагоналей относятся как 3 : 4. Найти площадь ромба. Ответ: 0,24  Решение
125. Определить сторону ромба, зная, что площадь его равна S, а длины диагоналей относятся как m : n. Ответ: 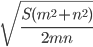 $\sqrt{\frac{S(m^2+n^2)}{2mn}}$ Решение
126. Периметр ромба равен 2р, а длины диагоналей относятся как m : n. Вычислить площадь ромба. Ответ: 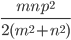$\frac{mnp^2}{2(m^2+n^2)}$  Решение
127. Высота ромба равна 12 см, а одна из его диагоналей равна 15 см. Найти площадь ромба. Ответ: 150  Решение
128. Высота ромба, проведенная из вершины тупого угла, делит его сторону на отрезки длиной m и n (m считать от вершины острого угла). Определить диагонали ромба. Ответ: 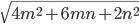 $\sqrt{4m^2+6mn+2n^2}$ Решение
129. Ромб, у которого сторона равна меньшей диагонали, равновелик кругу радиуса R. Определить сторону ромба. Ответ: 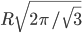$R\sqrt{2\pi/\sqrt{3}}$  Решение

130. В ромб с острым углом 30° вписан круг, а в круг — квадрат. Найти отношение площади ромба к площади квадрата. Ответ:  4 Решение

131. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиус окружностей. Ответ: 7,5  Решение
132. В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса 2. Найти сторону ромба. Ответ: 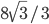$8\sqrt{3}/3$  Решение
133. Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такой четырехугольник есть ромб.
134. На сторонах ромба как на диаметрах описаны полуокружности, обращенные внутрь ромба. Определить площадь полученной розетки, если диагонали ромба равны а и b. Ответ: 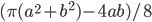$(\pi(a^2+b^2)-4ab)/8$  Решение
135. Периметр параллелограмма равен 90 см, а острый угол содержит 60°. Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма. Ответ: 15; 30  Решение
136. Величина одного из углов параллелограмма равна 60°, а меньшая диагональ 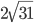$2\sqrt{31}$  см. Длина перпендикуляра, проведенного из точки пересечения диагоналей к большей стороне, равна 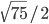$\sqrt{75}/2$ см. Найти длины сторон и большей диагонали параллелограмма. Ответ:  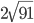$2\sqrt{91}$ Решение
137. Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15 см. Разность длин сторон параллелограмма равна 7 см. Найти длины сторон параллелограмма и его диагоналей. Ответ:  10, 17, 21, 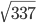$\sqrt{337}$ Решение
138. В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найти длины сторон параллелограмма. Ответ: 4; 12  Решение
139. В параллелограмме ABCD высота, проведенная из вершины В тупого угла на сторону DA, делит ее в отношении 5 : 3, считая от вершины D. Найти отношение AC : BD, если AD : AB = 2. Ответ: 2:1  Решение
140. Через точки R и E, принадлежащие сторонам АВ и AD параллелограмма ABCD и такие, что AR = 2 АВ /3, АЕ = AD/3, проведена прямая. Найти отношение площади параллелограмма к площади полученного треугольника. Ответ: 9  Решение
141. Доказать, что в параллелограмме ABCD расстояния от любой  точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон.
142. Доказать, что если через вершины четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемою этими прямыми, в 2 раза больше площади данного четырехугольника.
143. Две окружности радиуса R с центрами О₁ и О₂ касаются друг друга. Их пересекает прямая в точках А, В, С и D так, что АВ = ВС = CD. Найти площадь четырехугольника O₁ADO₂. Ответ: 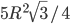 $5R^2\sqrt{3}/4$ Решение
144. В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимно перпендикулярны. Вычислить площадь фигуры О₁АВО₂, где АВ — общая касательная к окружностям, а О₁ и О₂ — их центры. Ответ: 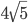$4\sqrt{5}$  Решение
145. Большее основание трапеции имеет длину 24 см. Найти длину ее меньшего основания, если известно, что расстояние между серединами диагоналей трапеции равно 4 см. Ответ: 16  Решение
146. Один из углов трапеции равен 30°, а прямые, содержащие боковые стороны трапеции, пересекаются под прямым углом. Найти длину меньшей боковой стороны трапеции, если ее средняя линия равна 10 см, а одно из оснований 8 см. Ответ:  2 Решение
147. Вычислить площадь трапеции, параллельные стороны которой содержат 16 и 44 см, а непараллельные — 17 и 25 см. Ответ: 450  Решение
148. Длины параллельных сторон трапеции равны 25 и 4 см, а длины непараллельных сторон — 20 и 13 см. Найти высоту трапеции. Ответ:   12 Решение
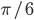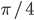149. Основания трапеции равны а и b, углы при большем основании равны $\pi/6$ и $\pi/4$. Найти площадь трапеции. Ответ: 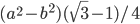$(a^2-b^2)(\sqrt{3}-1)/4$  Решение
150. Вычислить площадь трапеции ABCD (AD параллельно BC), если длины ее оснований относятся как 5 : 3 и площадь треугольника ADM равна 50 см², где М — точка пересечения прямых АВ и CD. Ответ: 32  Решение