Вступительный экзамен в ШАД 2014

Вступительный экзамен в Школу анализа данных
Международная зимняя школа по программированию
Харьков, Украина, 19 февраля 2014

Условия задач

1. Найдите все квадратные вещественные (то есть действительные - прим. www.itmathrepetitor.ru) матрицы порядка 3, удовлетворяющие уравнению $X^2+E=0$.
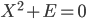2. Среди участников похода из любых четырех как минимум один знаком с тремя другими. Докажите, что каждый участник похода, кроме максимум трех, знаком со всеми остальными.
3. Опишите все невырожденные вещественные матрицы A, для которых все элементы матриц A и A⁻¹ неотрицательны.
4. Дан числовой массив длины n. Предложите алгоритм, находящий максимальное значение сумм отрезков этого массива. Ограничение по времени — O(n), по дополнительной памяти — O(1).
5. Есть 10 монет разного веса и некоторые весы. При помощи одного взвешивания на весах можно узнать для выбранных двух монет, какая тяжелее. Можно ли за 20 взвешиваний узнать, в каком порядке монеты идут по весу?
6. Вычислите сумму интегралов: $\int\limits_{\sqrt{\pi/6}}^{\sqrt{\pi/3}}\sin(x^2)dx$ + $\int\limits_{1/2}^{\sqrt{3}/2}\sqrt{arcsinx}dx$
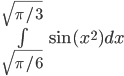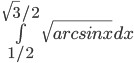
7. Игра состоит из одинаковых и независимых конов, в каждом из которых выигрыш происходит с вероятностью . Когда игрок выигрывает, он получает 1 доллар, а когда проигрывает — платит 1 доллар. Как только его капитал достигает величины долларов, он объявляется победителем и удаляется из казино. Найдите вероятность того, что игрок рано или поздно проиграет все деньги, в зависимости от его стартового капитала .
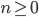8. Пусть $a$ - действительное число. Для каждого целого $n\ge 0$ обозначим через 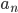$a_n$ расстояние до ближайшего рационального числа вида 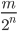$\displaystyle\frac{m}{2^n}$, где $m$ - целое. Найдите наибольшую возможную сумму ряда $\sum\limits_{n=0}^{\infty}a_n$.

Все материалы для подготовки

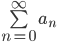смотрите еще Контрольная работа от Яндекс, март 2015 г. и Задачи вступительных экзаменов