Вступительный экзамен в ШАД 2015
 Июнь 2015
Июнь 2015
Условия задач
- Постройте график функции
![f(x)=\lim_{n\to+\infty}\sqrt[n]{1+x^n+(x^2/2)^n}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_848b945498d1cef8d2a744cc2a54820d.gif) ,
, 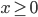
- Найдите собственные значения матрицы
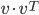 , где
, где 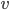 - некоторый вектор-столбец.
- некоторый вектор-столбец. - Найдите математическое ожидание числа неподвижных точек подстановки на
 элементах.
элементах. - Пусть
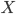 и
и 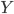 - квадратные матрицы одинакового размера, причем
- квадратные матрицы одинакового размера, причем 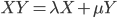 для некоторых
для некоторых 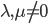 . Докажите, что матрицы
. Докажите, что матрицы 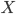 и
и 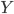 коммутируют.
коммутируют. - Электрическая цепь представляет собой связный неориентированный граф без кратных ребер, в котором ребра (числом
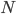 ) - это провода, а вершины - либо лампочки, либо единственный источник тока. На каждом ребре размещено реле. Лампочка горит, если существует путь, соединяющий ее с источником тока, вдоль которого все реле находятся в положении "включено". Известно, что ровно одно из реле бракованное и никогда не пропускает ток. Вы можете включать и отключать реле (и видите, горят ли лампочки). Изначально все выключатели находятся в положении "включено". Опишите способ нахождения неисправного реле за
) - это провода, а вершины - либо лампочки, либо единственный источник тока. На каждом ребре размещено реле. Лампочка горит, если существует путь, соединяющий ее с источником тока, вдоль которого все реле находятся в положении "включено". Известно, что ровно одно из реле бракованное и никогда не пропускает ток. Вы можете включать и отключать реле (и видите, горят ли лампочки). Изначально все выключатели находятся в положении "включено". Опишите способ нахождения неисправного реле за 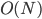 операций включения-выключения.
операций включения-выключения. - Пусть
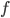 - дифференцируемая функция, причем
- дифференцируемая функция, причем 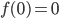 и
и  . Докажите, что для всех
. Докажите, что для всех 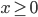 имеет неравенство
имеет неравенство 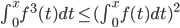 .
. - Для произвольных положительных
 и
и  вычислите сумму
вычислите сумму 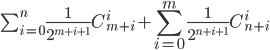 .
. - На сфере случайным образом выбираются четыре точки A, B, C и D. С какой вероятностью кратчайшие дуги AB и CD пересекаются?
смотрите еще Контрольная работа от Яндекс, март 2015 г. и Задачи вступительных экзаменов