Задачи по школьной математике. Окружность

Центральный угол АОВ на 30^о больше вписанного угла, опирающегося на дугу АВ. Найдите каждый из этих углов.
Хорды АВ и CD пересекаются в точке Е. Найдите ED, если: а) AE = 5, BE = 2, CE = 2,5; б) AE = 16, BE = 9, CE = ED; в) AE = 0,2, BE = 0,5, CE = 0,4.
Докажите, что дуги окружности, заключенные между параллельными хордами, равны.
Докажите, что хорда, перпендикулярная диаметру, длится точкой пересечения пополам.
В окружности с центром в точке О проведены два радиуса ОА и ОВ так, что расстояние от точки А до радиуса ОВ в два раза меньше длины радиуса. Найдите градусную меру вписанного угла, опирающегося на дугу АВ.
МА и МВ - хорды окружности с центром в точке О. Угол АМВ равен 30^о. Найдите длину хорды АВ, если радиус окружности равен 10.
Хорды АВ и CD окружности пересекаются в точке Е. Известно, что АЕ : ЕВ = 1 : 3, CD =20, DE = 5. Найдите АВ.
АВ - диаметр окружности. Точке Е лежит на окружности, ЕF перпендикулярно AB, FB = 4, EF = 6. Найдите радиус окружности.
Две хорды окружности взаимно перпендикулярны. Докажите, что расстояние от точки их пересечения до центра окружности равно расстоянию между их серединами.
В круге даны две взаимно перпендикулярные хорды. Каждая из них делится другой хордой на отрезки, равные a и b (a < b). Найдите расстояние от центра окружности до каждой хорды.
BM и CN - высоты треугольника ABC. Докажите, что точки B, N, M и C лежат на одной окружности.
Через точку A, лежащую на окружности, проведены диаметр AB и хорда AC, причем AC = 8 и угол BAC = 30◦. Найдите хорду CM, перпендикулярную AB.
Через концы диаметра окружности проведены две хорды, пересекающиеся на окружности и равные 12 и 16. Найдите расстояния от центра окружности до этих хорд.
На катете AC прямоугольного треугольника ABC как на диаметре построена окружность, пересекающая гипотенузу AB в точке K. Найдите CK, если AC = 2 и угол A = 30◦.
В окружности проведены хорды AB и CD. Расстояние между равными параллельными хордами AB и CD равно радиусу окружности. Найдите угол между пересекающимися прямыми AC и BD.
Продолжения хорд AB и CD окружности с диаметром AD пересекаются под углом 25◦. Найдите острый угол между хордами AC и BD.
Окружность, построенная на катете прямоугольного треугольника как на диаметре, делит гипотенузу пополам. Найдите углы треугольника.
Две прямые касаются окружности с центром O в точках A и B и пересекаются в точке C. Найдите угол между этими прямыми, если угол ABO = 40◦.
Две прямые, пересекающиеся в точке C, касаются окружности в точках A и B. Известно, что угол ACB = 120◦. Докажите, что сумма отрезков AC и BC равна отрезку OC.
Центр окружности, описанной около треугольника, совпадает с центром вписанной окружности. Найдите углы треугольника.
Точка D - середина гипотенузы AB прямоугольного треугольника ABC. Окружность, вписанная в треугольник ACD, касается отрезка CD в его середине. Найдите острые углы треугольника ABC.
Окружность вписана в треугольник со сторонами, равными a, b и c. Найдите отрезки, на которые точка касания делит сторону, равную a.
Окружность вписана в пятиугольник со сторонами, равными a, b, c, d и e. Найдите отрезки, на которые точка касания делит сторону, равную a.
Прямая касается окружности с центром O в точке A. Точка C на этой прямой и точка D на окружности расположены по разные стороны от прямой OA. Найдите угол CAD, если угол AOD равен 110◦.
Докажите, что если окружность касается всех сторон четырехугольника, то суммы противоположных сторон четырехугольника равны между собой.
В острый угол, равный 60◦, вписаны две окружности, касающиеся друг друга внешним образом. Радиус меньшей окружности равен r. Найдите радиус большей окружности.
Окружность, построенная на стороне AD параллелограмма ABCD как на диаметре, проходит через вершину B и середину стороны BC. Найдите углы параллелограмма.
Дана окружность с центром в точке O и радиусом 2. Из конца отрезка OA, пересекающегося с окружностью в точке M, проведена касательная AK к окружности (K - точка касания), угол OAK = 60◦. Найдите радиус окружности, касающейся отрезков AK, AM и дуги MK.
К двум окружностям, касающимся внешним образом в точке C, проведена общая внешняя касательная, A и B - точки касания. Найдите радиусы окружностей, если AC = 6, ВС = 8.
Три окружности радиусов 1, 2 и 3 касаются друг друга внешним образом. Найдите радиус окружности, проходящей через точки касания этих окружностей.
Окружность с центром на гипотенузе прямоугольного треугольника касается катетов. Найдите радиус окружности, если катеты равны a и b.
Окружность касается стороны треугольника, равной a, и продолжения двух других сторон. Докажите, что радиус окружности равен площади треугольника, деленной на разность между полупериметром и стороной a.
В треугольник АВС со сторонами АВ = с, ВС = а, АС = b вписана окружность, и к ней проведена касательная, пересекающая стороны АВ и ВС соответственно в точках М и N. Найдите периметр треугольника MBN.
В треугольник с периметром 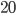$20$ вписана окружность. Отрезок касательной, проведенной к окружности параллельно основанию, заключенной между сторонами треугольника, равен 14/5. Найдите основание треугольника.
Пусть a и b — длины катетов прямоугольного треугольника, c — длина его гипотенузы. Докажите, что радиус окружности, касающейся гипотенузы и продолжений катетов, равен (a + b + c)/2
Вписанный угол на 20^о меньше центрального угла, опирающегося на ту же хорду. Найдите эти углы.
Хорды AB и CD пересекаются в точке О так, что непересекающиеся дуги AC и BD соответственно равны 40^о и 60^о. Найдите угол АОС.
Из точки В, взятой на окружности, проведены диаметр ВС и хорда ВА, которая стягивает дугу в 46^о. Найдите угол между диаметром и хордой.
Хорды AB и BC взаимно перпендикулярны. Найдите угол ВСА, если хорда BC стягивает дугу в 53^о.
Расстояние от центра окружности до хорды равно 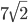$7\sqrt{2}$ и вдвое меньше длины хорды. Найдите радиус окружности.
Внутри окружности на расстоянии 15 от центра дана точка. Хорда делится этой точкой на отрезки 7 и 25. Найдите радиус хорды.
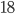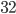В окружности перпендикулярно диаметру АВ проведена хорда CD. Точка их пересечения делит диаметр на отрезки длиной $18$ и $32$ . Найдите длину хорды CD.
Диаметр AB пересекает хорду CD и делит ее на два отрезка, равных 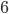$6$ . Найдите ВС, если радиус окружности равен 6,25.
Внутри окружности радиуса 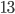$13$ дана точка М, которая удалена от центра окружности на 5. Через точку М проведена хорда АВ длиной 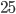$25$ . Найдите отрезки, на которые хорда АВ делится точкой М.
К окружности из точки А проведены касательная АВ и секущая ACD. Найдите хорду CD, если отрезки AB и AD соответственно равны 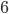$6$ и $9$ .
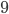На касательной к окружности по обе стороны от точки касания отмечены точки А и В, удаленные от центра окружности на расстояние, равное 20. Найдите радиус окружности, если отрезок АВ равен 32.
Через точку В проведены касательная ВС и секущая BDA к окружности с диаметром АС. Найдите CD, если AB равно 16 и площадь треугольника АВС равна 8.
Из точки А проведены две касательные к окружности, радиус которой равен 6. Найдите расстояние от точки А до хорды соединяющей точки касания, если угол между касательными равен 120^о.
Через точку А, лежащую вне окружности, проведены касательная АВ и секущая CD. Найдите АВ, если радиус окружности равен 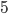$5$ , расстояние от центра окружности до хорды CD равно 3 и АС равно 1.
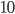Через точку, лежащую вне окружности, проведены секущая и две касательные. Сумма длин касательных равна 24. Найдите длину внешнего отрезка секущей, если длина ее внутреннего отрезка равна $10$ .