1. Преобразовать в многочлен:
1) 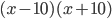 ;
;
2) 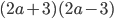 ;
;
3) 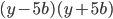 ;
;
4) 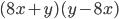 ;
;
5) 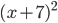 ;
;
6) 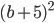 ;
;
7) 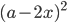 ;
;
8) 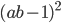 ;
;
9) 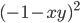 ;
;
10)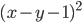 ;
;
2. Разложить на множители:
1) 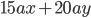 ;
;
2) 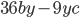 ;
;
3) 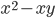 ;
;
4) 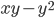 ;
;
5) 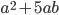 ;
;
6) 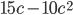 ;
;
7) 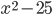 ;
;
8)  ;
;
9) 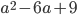 ;
;
10) 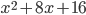 ;
;
11) 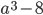 ;
;
12) 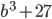 ;
;
13) 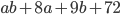 ;
;
14) 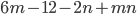 ;
;
15) 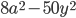 ;
;
16) 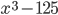 ;
;
3. Указать допустимые значения переменной в выражении:
1) 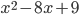 ;
;
2) 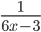 ;
;
3) 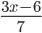 ;
;
4) 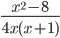 ;
;
5) 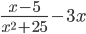 ;
;
6) 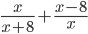 ;
;
4. Сократить:
1) 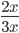 ;
;
2) 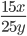 ;
;
3) 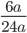 ;
;
4) 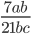 ;
;
5) 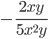 ;
;
6) 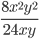 ;
;
7) 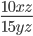 ;
;
8) 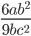 ;
;
9) 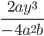 ;
;
10) 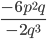 ;
;
11) 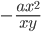 ;
;
12) 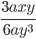 ;
;
13) 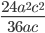 ;
;
14) 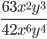 ;
;
15) 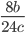 ;
;
16) 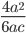 ;
;
17) 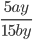 ;
;
18) 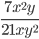 ;
;
19) 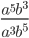 ;
;
20) 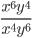 ;
;
21) 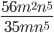 ;
;
22) 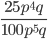 ;
;
23) 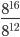 ;
;
24) 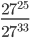 ;
;
25) 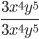 ;
;
5. Упростить:
1) 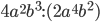 ;
;
2) 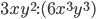 ;
;
3) 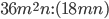 ;
;
4) 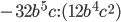 ;
;
5) 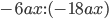 ;
;
6) 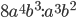 ;
;
7) 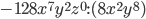 ;
;
8) 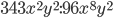 ;
;
9) 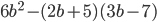 ;
;
10) 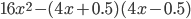 ;
;
11) 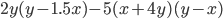 ;
;
12) 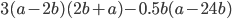 ;
;
13) 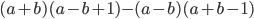 ;
;
14) 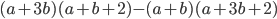 ;
;
15) 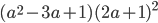 ;
;
16) 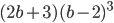 ;
;
17) 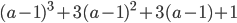 ;
;
18) 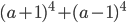 ;
;
19) 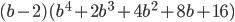 ;
;
20) 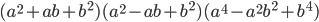 ;
;
21) 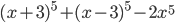 ;
;
6. Упростить:
1) 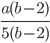 ;
;
2) 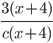 ;
;
3) 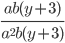 ;
;
4) 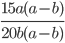 ;
;
5) 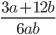 ;
;
6) 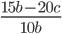 ;
;
7) 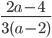 ;
;
8) 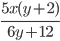 ;
;
9) 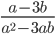 ;
;
10) 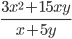 ;
;
11) 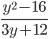 ;
;
12) 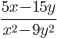 ;
;
13) 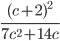 ;
;
14) 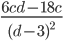 ;
;
15) 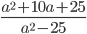 ;
;
16) 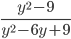 ;
;
17) 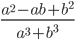 ;
;
18) 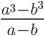 ;
;
19) 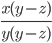 ;
;
20) 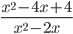 ;
;
21) 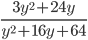 ;
;
22) 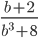 ;
;
23) 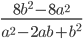 ;
;
24) 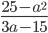 ;
;
25) 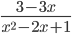 ;
;
26) 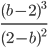 ;
;
27) 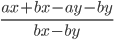 ;
;
28) 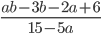 ;
;
29) 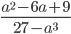 ;
;
30) 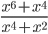 ;
;
31) 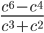 ;
;
32) 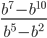 ;
;
33) 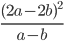 ;
;
34) 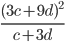 ;
;
35) 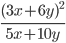 ;
;
36) 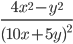 ;
;
7. Найти значение дроби:
1) 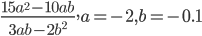 ;
;
2) 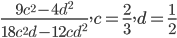 ;
;
3) 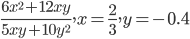 ;
;
4) 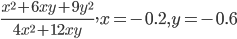 ;
;
8. Выполнить действие:
1) 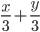 ;
;
2) 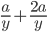 ;
;
3) 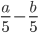 ;
;
4) 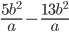 ;
;
5) 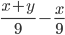 ;
;
6) 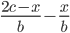 ;
;
7) 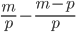 ;
;
8) 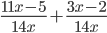 ; 9)
; 9)
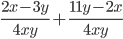 ; 10)
; 10)
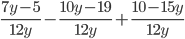 ; 11)
; 11)
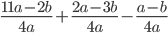 ;
;
12) 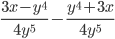 ;
;
13) 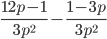 ;
;
14) 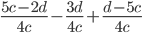 ;
;
15) 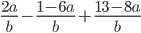 ;
;
16) 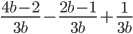 ;
;
17) 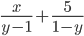 ;
;
18) 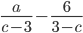 ;
;
19) 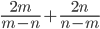 ;
;
20) 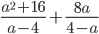 ;
;
21) 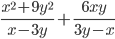 ;
;
9. Пользуясь равенством 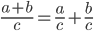 , представить в виде суммы или разности дробей:
, представить в виде суммы или разности дробей:
1) 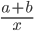 ;
;
2) 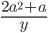 ;
;
3) 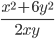 ;
;
4) 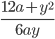 ;
;
5) 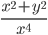 ;
;
6) 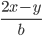 ;
;
7) 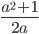 ;
;
8) 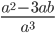 ;
;
6.23) 8(a+b)/(b-a)
6.24) -(5+a)/3
6.25) 3/(1-x)
6.26) b-2
6.27) (a+b)/b
6.28) (2-b)/5
6.29) (3-a)/(a*a+3a+9)
6.30) x*x
6.31) c*c*(c-1)
6.32) -b^5
6.33) 4(a+b)