ЕГЭ 2015 Досрочный вариант по математике 11 класс
Условия задач с ответами и решениями
- Бегун пробежал 180 метров за 20 секунд. Найдите среднюю скорость бегуна. Ответ дайте в километрах в час.
- На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало 5 миллиметров осадков.

- Телефонная компания предоставляет на выбор три тарифных плана. Абонент предполагает, что общая длительность разговоров составит 700 минут в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей должен будет заплатить абонент за месяц, если общая длительность разговоров действительно будет равна 700 минутам?
Тарифный план Абонентская плата (за месяц) Плата за 1 минуту разговора Повременный нет 0,3 руб Комбинированный 160 руб. за 420 мин 0,2 руб (сверх 420 мин) Безлимитный 255 руб нет - На клетчатой бумаге с размером клетки 1х1 изображен угол. Найдите синус этого угла.

- Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
- Найдите корень уравнения
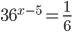
- Периметр прямоугольной трапеции, описанной около окружности, равен 32, ее большая боковая сторона равна 9. Найдите радиус окружности.
- На рисунке изображён график функции и шесть точек на оси абсцисс:
 . В скольких из этих точек производная функции отрицательна?
. В скольких из этих точек производная функции отрицательна? 
- В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите ее объем.
- Вычислите
![\displaystyle\frac{\sqrt[28]{3}\cdot 3\cdot\sqrt[21]{3}}{\sqrt[12]{3}}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_7094c03471f8f8ec27ee6a8742f44286.gif)
- Водолазный колокол, содержащий
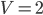 моля воздуха при давлении
моля воздуха при давлении 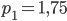 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления
атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления 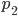 . Работа, совершаемая водой при сжатии воздуха, определяется выражением
. Работа, совершаемая водой при сжатии воздуха, определяется выражением 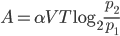 , где
, где 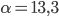 Дж/(моль
Дж/(моль К) — постоянная,
К) — постоянная, 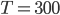 K — температура воздуха. Найдите, какое давление (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15960 Дж.
K — температура воздуха. Найдите, какое давление (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15960 Дж. - Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37.
- Смешав 43‐процентный и 89‐процентный растворы кислоты и добавив 10 кг чистой воды, получили 69‐процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50‐процентного раствора той же кислоты, то получили бы 73‐процентный раствор кислоты. Сколько килограммов 43‐процентного раствора использовали для получения смеси?
- Найдите наибольшее значение функции
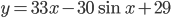 на отрезке
на отрезке ![\displaystyle [-\frac{\pi}{2}; 0]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_9085c4924a7d200873662be3f4bc4f45.gif) Решение
Решение - а) Решите уравнение
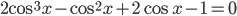 ; б) Укажите корни этого уравнения, принадлежащие отрезку
; б) Укажите корни этого уравнения, принадлежащие отрезку ![[2\pi; \frac{7\pi}{2}]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_36fcfd780e97f1754b7cb743e1a91b49.gif) . Решение
. Решение - В кубе
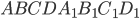 все ребра равны 5. На отрезке
все ребра равны 5. На отрезке 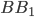 отмечена точка
отмечена точка 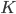 так, что
так, что 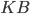 равно 3. Через точки
равно 3. Через точки 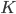 и
и 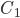 проведена плоскость
проведена плоскость  , параллельная прямой
, параллельная прямой 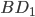 . а) Докажите, что
. а) Докажите, что 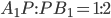 , где
, где  - точка пересечения плоскости
- точка пересечения плоскости  с ребром
с ребром  ; б) Найдите объем большей из двух частей куба, на которые он делится плоскостью
; б) Найдите объем большей из двух частей куба, на которые он делится плоскостью  . Решение
. Решение - Решите неравенство
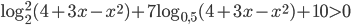 Решение
Решение - К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. а) Докажите, что периметр треугольника AMN равен стороне квадрата. б) Прямая MN пересекает прямую CD в точке P. Найдите отношение, в котором делится сторона BC прямой, проходящей через точку P и центр окружности, если известно, что AM : MB = 1 : 2. Решение
- Петя является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе первого города трудятся суммарно
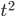 часов в неделю, то за эту неделю они производят
часов в неделю, то за эту неделю они производят 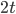 единиц товара, а рабочие на заводе второго города, если суммарно трудятся
единиц товара, а рабочие на заводе второго города, если суммарно трудятся 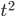 часов в неделю, то производят
часов в неделю, то производят 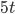 единиц товара за эту неделю. На обоих заводах за каждый час работы Петя платит рабочему 500 руб. Какую наименьшую сумму придется тратить на оплату рабочим в неделю, чтобы производилось 580 единиц товара в неделю? Решение
единиц товара за эту неделю. На обоих заводах за каждый час работы Петя платит рабочему 500 руб. Какую наименьшую сумму придется тратить на оплату рабочим в неделю, чтобы производилось 580 единиц товара в неделю? Решение - Найдите все значения параметра
 , при каждом из которых система уравнений
, при каждом из которых система уравнений 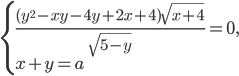 имеет единственное решение. Решение
имеет единственное решение. Решение - На доске написано несколько двузначных натуральных чисел, не содержащих нулей. Сумма этих чисел равна 2970. В каждом числе поменяли местами первую и вторую цифры (например, 23 заменили на число 32). а) Приведите пример исходных чисел, для которых сумма получившихся после перестановки цифр чисел ровно в 3 раза меньше суммы исходных чисел; б) Могла ли сумма получившихся чисел быть ровно в 5 раз меньше суммы исходных чисел? в) Найдите наименьшее возможное значение суммы получившихся чисел. Решение
смотрите также Досрочный ЕГЭ по математике 2014
Ответы
- 32,4
- 11
- 210
- 4/5
- 0,15
- 9/2
- 7/2
- 2
- 32
- 3
- 7
- 74
- 35
- 29
- а)
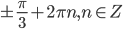 б)
б) 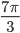
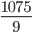
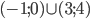
- 1:2
- 5800000
![(-\infty; -6]\cup](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a9fb2f0915c2c559d22e8828bbdb5c0e.gif) {
{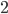 }
}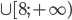
- а) один из вариантов ответа: 32 раза число 92 и число 26; б) нет; в) 693

В 4 задании дается угол в 135 градусов (90 и +45 если разбить на 2 угла = 135), Синус 135 корень из 2 :2 = 0.7, а не 4/5 (4/5= 0.8) (кроень из 2 =1,414....,а деленное на 2 0.707.... и в итоге 0.7 должно быть
вы ошибаетесь. там не 135 градусов