Варианты вступительных экзаменов по математике в МГУ на факультет почвоведения.
Факультет почвоведения МГУ, 2000 г.
- Решите неравенство
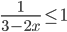 .
. - Первый, второй и четвертый члены арифметической прогрессии одновременно являются соответственно первым, вторым и третьим членами некоторой геометрической прогрессии. Найдите все значения, которые может принимать знаменатель геометрической прогрессии.
- Найдите
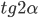 , если известно, что
, если известно, что 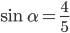 , а
, а 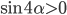 .
. - Решите неравенство
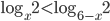 .
. - Решите уравнение
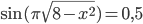 .
. - Биссектрисы внутренних углов треугольника продолжены до точек пересечения с описанной около треугольника окружностью, отличных от вершин исходного треугольника. В результате попарного соединения этих точек получился новый треугольник. Известно, что углы исходного треугольника равны 30, 60 и 90 градусов, а его площадь равна 2. Найдите площадь нового треугольника.
- Найдите все значения параметра
 , при которых при любых значениях параметра
, при которых при любых значениях параметра  уравнение
уравнение 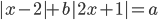 имеет хотя бы одно решение.
имеет хотя бы одно решение.
Факультет почвоведения МГУ, 2001 г.
- Решите уравнение
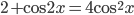 .
. - Решите уравнение
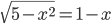 .
. - Решите неравенство
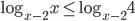 .
. - В треугольнике ABC боковые стороны AB и BC равны. Основание AC равно 2, а угол при основании равен 30 градусам. Из вершины А к боковой стороне BC проведены биссектриса AE и медиана AD. Найдите площадь треугольника ADE.
- Решите неравенство
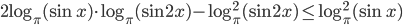 .
. - Дано задание: на прямоугольном участке земли размером 1 м на 4 м посадить три дерева, одно из которых должно быть в углу участка. Расстояние между любыми двумя деревьями не должно быть меньше 2,5 м. Можно ли выполнить это задание? Ответ обосновать.
Ответы
2000 г.
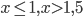
- 1; 2
- 24/7
- 0<x<1, 3<x<5
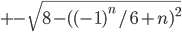 , n=0,1,2
, n=0,1,2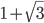
- 5/2
2001 г.
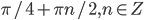
- -1
- (3; 4]
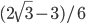
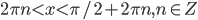
- нельзя