Вступительное испытание
по математике в МГУ 2019 года
1 июля 2019 г
Экономический факультет
Вариант 1
- Решите уравнение
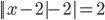
- Решите неравенство
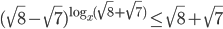
- Решите уравнение
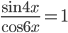
- Решите уравнение
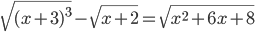
- В правильной треугольной пирамиде SABC длина стороны основания ABC равна 2, длина боковой стороны равна 3. Точка P - проекция вершины B на плоскость SAC. Найдите площадь треугольника CSP.
- Из пункта А в пункт В вышел пешеход. Вслед за ним через 2 часа из А выехал велосипедист, а еще через полчаса - мотоциклист. Все трое двигались с постоянными скоростями. Мотоциклист обогнал в пути пешехода и велосипедиста и через некоторое время сделал остановку в пункте С. Пешеход и велосипедист одновременно достигли пункта С на 3 минуты позже мотоциклиста и сразу после этого все трое продолжили движение. На сколько времени (в часах) раньше пешехода в пункт В прибыл велосипедист, если пешеход прибыл туда на 1 час позже мотоциклиста?
- В трапеции ABCD длина боковой стороны CD равна 2, расстояния от точек А и В до CD равны
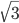 и
и 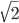 соответственно. Найдите площадь треугольника ABD.
соответственно. Найдите площадь треугольника ABD. - Максимальное значение выражения
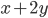 при условии
при условии 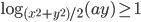 равно 4. Чему равно положительное значение параметра
равно 4. Чему равно положительное значение параметра  ?
?
Ответы
смотрите еще Вступительные экзамены и МГУ. Дополнительное вступительное испытание 2013
