Теория чисел
Задачи 181-200

- Решите уравнение
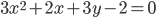 в целых числах
в целых числах - Найдите целые положительные решения уравнения
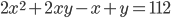
- Найдите все целочисленные решения уравнения
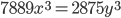 , если
, если 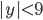
- Решите уравнение в целых числах
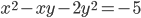
- Найдите все целые решения уравнения
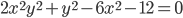
- Найдите все целые решения уравнения
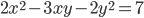
- Решите в целых числах уравнение
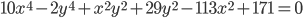
- Найдите все пары целых чисел
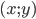 , удовлетворяющие уравнению
, удовлетворяющие уравнению 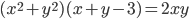
- Докажите, что
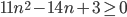 при
при 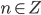
- Найдите целые
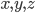 такие, что
такие, что 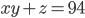 и
и 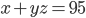
- Найдите все целые числа
 и
и  такие, что
такие, что 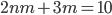 и
и 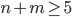
- Найдите все пары целых чисел
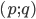 , удовлетворяющие одновременно неравенствам
, удовлетворяющие одновременно неравенствам 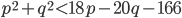 и
и 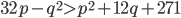
- Найдите все пары целых чисел
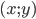 такие, что
такие, что 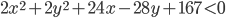 и
и 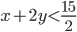
- В школьной газете сообщается, что процент учеников некоторого класса, повысивших во втором полугодии успеваемость, заключен в пределах от 2,9% до 3,1%. Определите минимально возможное число учеников в таком классе.
- В контейнер упакованы изделия двух типов. Стоимость и вес одного изделия составляют 400 тыс. руб. и 12 кг для первого типа и 600 тыс. руб. и 15 кг для второго. Общий вес изделий 321 кг. Определите минимальную и максимальную возможную стоимость находящихся в контейнере изделий
- В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес одного изделия составляют 400 тыс. руб. и 12 кг для первого типа, 500 тыс. руб. и 16 кг - для второго типа, 600 тыс. руб. и 15 кг - для третьего типа. Общий вес изделий равен 326 кг. Определите минимальную и максимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
- Натуральные числа
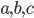 , взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2240 и 4312 делятся без остатка на
, взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2240 и 4312 делятся без остатка на  и
и  соответственно. Найдите числа
соответственно. Найдите числа 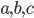 , если известно, что при указанных условиях сумма
, если известно, что при указанных условиях сумма 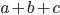 максимальна.
максимальна. - Решите в целых числах уравнение
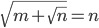
- Решите в целых числах уравнение
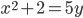
- Докажите, что если числа
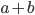 и
и 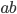 рациональны, то число
рациональны, то число 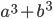 также рационально.
также рационально.