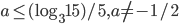Урок 38. [3] Более сложные логические задачи
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- Найдите все
 , при которых уравнение
, при которых уравнение 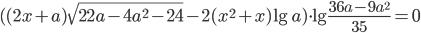 имеет по крайней мере два корня, один из которых
имеет по крайней мере два корня, один из которых 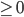 , а другой
, а другой 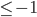 .
. - Найдите все
 , при которых система
, при которых система 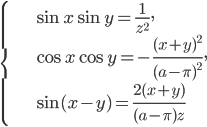 имеет ровно одно решение, удовлетворяющее условиям
имеет ровно одно решение, удовлетворяющее условиям 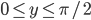 и
и 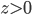 .
. - Даны системы
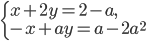 и
и 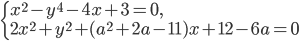 . При каких
. При каких  они равносильны?
они равносильны? - При каких
 система
система 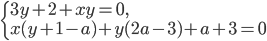 имеет единственное решение?
имеет единственное решение? - При каких
 неравенство
неравенство 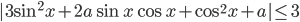 выполнено для любого
выполнено для любого  ?
? - Найдите все
 , при которых система
, при которых система 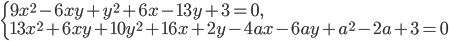 имеет хотя бы одно решение.
имеет хотя бы одно решение. - Найдите все
 , при которых неравенство
, при которых неравенство 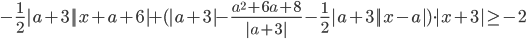 выполняется ровно для двух значений
выполняется ровно для двух значений  .
. - При каких
 уравнение
уравнение 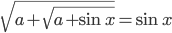 имеет решение?
имеет решение? - При каких
 система
система 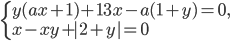 имеет решения?
имеет решения? - При каких
 ровно одно решение неравенства
ровно одно решение неравенства 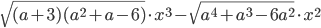
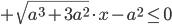 удовлетворяет условию
удовлетворяет условию 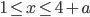 ?
? - При каком
 система неравенств
система неравенств 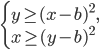 имеет единственное решение?
имеет единственное решение? - Найдите все числа
 и
и 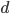 , для которых наибольшее значение функции
, для которых наибольшее значение функции 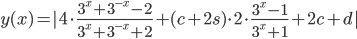 на отрезке [-1; 1] является наименьшим.
на отрезке [-1; 1] является наименьшим. - Найдите все
 , при которых система
, при которых система 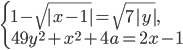 имеет ровно четыре решения.
имеет ровно четыре решения. - Найдите все пары (a;b), для которых система
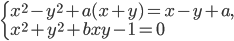 имеет не менее пяти решений (x; y).
имеет не менее пяти решений (x; y). - Найдите все
 такие, что система
такие, что система 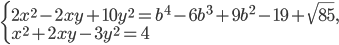 имеет хотя бы одно решение.
имеет хотя бы одно решение. - Найдите все
![b\in [-1;1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_2e5f21fdfe0226a26ac09bc23410d736.gif) такие, что выражение
такие, что выражение 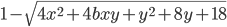 принимает наибольшее значение лишь при одной паре (x; y).
принимает наибольшее значение лишь при одной паре (x; y). - При каких
 уравнение
уравнение 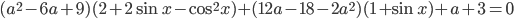 не имеет решений?
не имеет решений? - При каких
 уравнение
уравнение 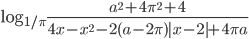
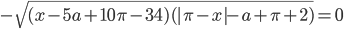 имеет хотя бы одно целочисленное решение?
имеет хотя бы одно целочисленное решение? - Найдите все
 , при которых система уравнений
, при которых система уравнений 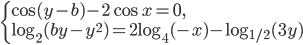 имеет нечетное число решений.
имеет нечетное число решений. - Найдите все
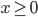 , при которых из неравенств
, при которых из неравенств 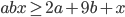 ,
, 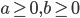 следует неравенство
следует неравенство 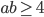 .
. - Найдите все
 , при которых наименьшее значение квадратного трехчлена
, при которых наименьшее значение квадратного трехчлена 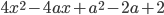 на отрезке [0; 2] равно 3.
на отрезке [0; 2] равно 3. - При каких p уравнение
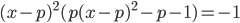 имеет больше положительных корней, чем отрицательных?
имеет больше положительных корней, чем отрицательных? - При каких
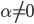 количество пар (x; y) целых чисел таких, что
количество пар (x; y) целых чисел таких, что 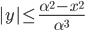 минимально?
минимально? - При каких
 число решений уравнения
число решений уравнения 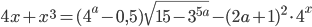 меньше числа решений уравнения
меньше числа решений уравнения 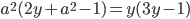 ?
?
Ответы к домашнему заданию урока 38 из В.В. Ткачук "Математика - абитуриенту"
- {3/2}U{5/3}U[2;4)
![[-2\pi;0)\cup (2\pi; 4\pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_44ec0763f3e1674fba5ab2f09148b60f.gif)
- -2; -1
- 1; 3; 11/12
- [-12/5; 0]
![[2/3-\sqrt{2}; 2/3+\sqrt{2}]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_b7a75bccfd011fab620ec466695976a7.gif)
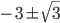
- [-1/4; 0]
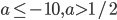
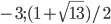
- -1/4
- -1/3; 1/6
- -1/4; -1/32
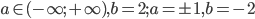
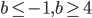
- [-1/3; 1/3]
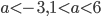
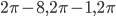
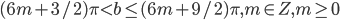
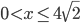
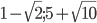
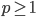
- (1/2; 1) U (1;2)