Вступительный экзамен в ШАД 25 мая 2014

Вступительный экзамен в Школу анализа данных
25 мая 2014

Экзамен длится 4 часа

Условия задач

Пусть 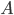$A$ - квадратная матрица, у которой сумма матричных элементов в каждом столбце равна 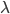$\lambda$ . Докажите, что 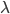$\lambda$ является собственным значением матрицы $A$ .
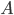На плоскости зафиксированы две точки A и B на расстоянии 2. Пусть C - случайно выбранная точка круга радиуса R с центром в середине отрезка AB. С какой вероятностью треугольник ABC будет тупоугольным?
Требуется отгадать число от 1 до n (n>10), задавая лишь вопросы, на которые можно отвечать "да" или "нет"; при этом отвечающий может один раз солгать. Придумайте алгоритм, гарантированно позволяющий сделать это быстрее, чем 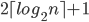$2\lceil log_2 n\rceil+1$ за шагов.
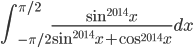
Найдите интеграл $\int_{-\pi/2}^{\pi/2}\displaystyle\frac{\sin^{2014}x}{\sin^{2014}x+\cos^{2014}x}dx$
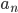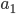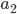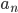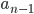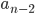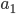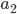
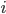Зададим числовую последовательность $a_n$ следующим образом. Пусть $a_1$ и $a_2$ - произвольные натуральные числа. Число $a_n$ получается приписыванием к $a_{n-1}$ числа $a_{n-2}$ справа. Предложите алгоритм, вычисляющий по данным $a_1$ и $a_2$ $i$ -ю цифру числа 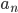$a_n$ и оцените его временную сложность. Ограничение по памяти: O(1).
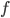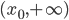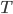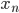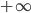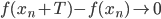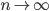Пусть функция $f$ непрерывна и ограничена на промежутке $(x_0,+\infty)$ . Докажите, что для любого числа $T$ существует последовательность { $x_n$ }, стремящиеся к $+\infty$ и такая, что $f(x_n+T)-f(x_n)\to0$ при $n\to\infty$ .
Найдите максимальное значение определителя матрицы (а) второго (б) третьего порядка, если сумма квадратов всех ее элементов не превосходит 1.
В компании из 51 человека каждый на дух не переносит ровно троих (при этом они не обязательно отвечают ему взаимностью). Требуется разделить компанию на n групп так, чтобы каждый человек входил только в одну группу, и между членами каждой из групп царило взаимопонимание. При каком наименьшем n это возможно?