Решение тренировочной работы по математике
МИОО 24 сентября 2015 г
13. Материал сайта www.itmathrepetitor.ru а) Из уравнения 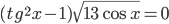 следует, что
следует, что 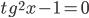 или
или 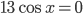 . При этом помним, что и тангенс, и квадратный корень должны существовать. Поэтому второе уравнение
. При этом помним, что и тангенс, и квадратный корень должны существовать. Поэтому второе уравнение 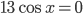 можно не рассматривать, так как
можно не рассматривать, так как 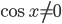 из-за тангенса. Остается решить уравнение
из-за тангенса. Остается решить уравнение 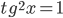 с ограничением
с ограничением 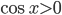 из-за квадратного корня. Получаем
из-за квадратного корня. Получаем 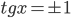 и
и 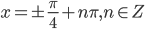 . Из этого множества углов оставляем только те, которые принадлежат I или IV четверти. Поэтому
. Из этого множества углов оставляем только те, которые принадлежат I или IV четверти. Поэтому 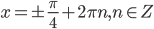 .
.
б) Материал сайта www.itmathrepetitor.ru В этом пункте необходимо из найденного множества корней выбрать только те, которые принадлежат отрезку ![[-3\pi; -3\pi/2]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_4029140917fa79c7e0488f25f50cd403.gif) . Так как корни заданы довольно простой формулой, то можно попробовать определить углы "на глаз". Но применим более общий способ, чтобы на экзамене быть во всеоружии. Разобьем формулу
. Так как корни заданы довольно простой формулой, то можно попробовать определить углы "на глаз". Но применим более общий способ, чтобы на экзамене быть во всеоружии. Разобьем формулу 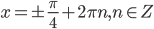 на две более простых
на две более простых 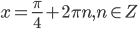 и
и 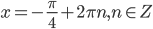 и каждую поместим в двойное неравенство. То есть
и каждую поместим в двойное неравенство. То есть 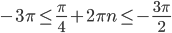 и
и 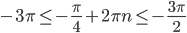 .
.
Решим первое неравенство (второе рассмотрите самостоятельно). Домножим все три части на 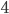 и перенесем
и перенесем 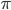 из средней части в крайние (слагаемое
из средней части в крайние (слагаемое 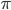 поменяет знак и появится в обеих частях, что кажется странным, ибо было одно слагаемое, а стало два, но ошибки здесь нет):
поменяет знак и появится в обеих частях, что кажется странным, ибо было одно слагаемое, а стало два, но ошибки здесь нет): 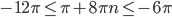
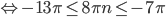 , откуда
, откуда 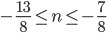 . Так как
. Так как 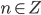 , то есть
, то есть  - целое число, то
- целое число, то 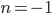 . Подставляем это значение в формулу
. Подставляем это значение в формулу 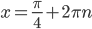 и получаем, что
и получаем, что 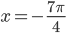 . Из второй формулы получим угол, равный
. Из второй формулы получим угол, равный 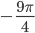 .
.
15.1. Перед решением полезно вспомнить, что 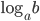 существует только при
существует только при  , что
, что 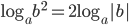 и что
и что 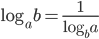 . Подробности можно посмотреть в справочнике.
. Подробности можно посмотреть в справочнике.
Заметим, что 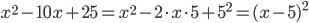 и
и 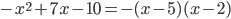 . Здесь мы использовали формулы сокращенного умножения (квадрат разности и формула разложения квадратного трехчлена). Поэтому неравенство принимает вид
. Здесь мы использовали формулы сокращенного умножения (квадрат разности и формула разложения квадратного трехчлена). Поэтому неравенство принимает вид 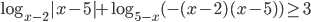 . Типичной ошибкой было бы забыть про модуль.
. Типичной ошибкой было бы забыть про модуль.
Далее из существования второго слагаемого следует, что 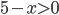 , значит, подмодульное выражение положительно и
, значит, подмодульное выражение положительно и 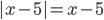 . Материал сайта www.itmathrepetitor.ru
. Материал сайта www.itmathrepetitor.ru
Рассмотрим второе слагаемое. Можно формально применить свойство 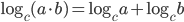 и получить, например, выражение
и получить, например, выражение 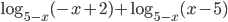 . И здесь будет допущена ошибка, связанная с тем, что в свойстве
. И здесь будет допущена ошибка, связанная с тем, что в свойстве 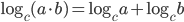 неявно предполагается, что все три логарифма существуют, то есть
неявно предполагается, что все три логарифма существуют, то есть 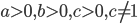 . В противном случае формулу применять нельзя. В нашем примере
. В противном случае формулу применять нельзя. В нашем примере 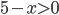 и
и 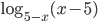 не существует. Поэтому предварительно запишем логарифм в виде
не существует. Поэтому предварительно запишем логарифм в виде 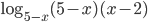 . Теперь обе скобки положительны и уравнение принимает вид
. Теперь обе скобки положительны и уравнение принимает вид 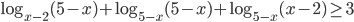
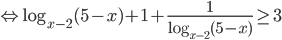
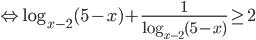 .
.
Пусть 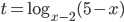 , тогда
, тогда 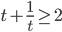
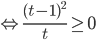 , откуда
, откуда 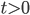 . Возвратимся к замене.
. Возвратимся к замене.
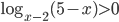
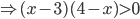
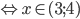 . При этом хотя бы устно необходимо проверить ограничения на
. При этом хотя бы устно необходимо проверить ограничения на  из исходного неравенства.
из исходного неравенства.
15.2 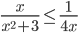
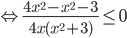 . Заметим, что множитель
. Заметим, что множитель 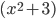 можно удалить из знаменателя, так как он положителен и знак дроби зависит только от остальных множителей. Приходим к неравенству
можно удалить из знаменателя, так как он положителен и знак дроби зависит только от остальных множителей. Приходим к неравенству 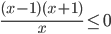 .
.

Откуда методом интервалов находим ответ ![x\in (-\infty;-1]\cup (0;1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_ceadec995b864eb06602e7bf2e2c13ee.gif)
17. www.itmathrepetitor.ru Прибыль за один год равна 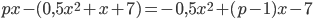 млн. руб. Данное выражение является квадратным трехчленом с отрицательным коэффициентом
млн. руб. Данное выражение является квадратным трехчленом с отрицательным коэффициентом 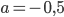 , поэтому его наибольшее значение существует (ветви параболы направлены вниз) и достигается при
, поэтому его наибольшее значение существует (ветви параболы направлены вниз) и достигается при 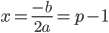 (по формуле нахождения абсциссы вершины параболы). А наибольшее значение равно
(по формуле нахождения абсциссы вершины параболы). А наибольшее значение равно 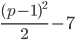 (определили банальной подстановкой
(определили банальной подстановкой  в формулу прибыли). Тогда
в формулу прибыли). Тогда 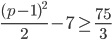 , откуда
, откуда 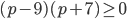 . Так как цена
. Так как цена  не может быть отрицательной, то
не может быть отрицательной, то 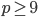 . Значит, наименьшее значение равно
. Значит, наименьшее значение равно 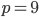 .
.
смотрите еще Демонстрационный вариант КИМ для проведения в 2016 году ЕГЭ по математике 11 класс Профильный уровень
