Варианты вступительных экзаменов по математике в МГУ на физический факультет.
Физический факультет МГУ, 2003 г.
- Решите уравнение
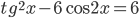 .
. - Решите неравенство
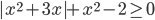 .
. - Решите неравенство
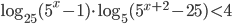 .
. - В трапеции KLMN с основаниями LM и KN точка А - середина отрезка MN, LA - биссектриса угла KLM, средняя линия равна
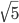 , KA = 4. Найдите LA.
, KA = 4. Найдите LA. - Решите систему уравнений
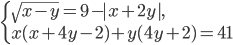 .
. - В треугольнике KLM радиус описанной окружности равен R, угол К равен
 , точка О - центр окружности, вписанной в этот треугольник. Прямая КО пересекает окружность, описанную около треугольника KLM, в точке N. Найдите ON.
, точка О - центр окружности, вписанной в этот треугольник. Прямая КО пересекает окружность, описанную около треугольника KLM, в точке N. Найдите ON. - Для каждого значения
 решите неравенство
решите неравенство 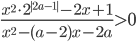 .
. - В пирамиде SLMN даны ребра: LM = 5, MN = 9, NL = 10. Сфера радиуса
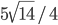 касается плоскости основания LMN и боковых ребер пирамиды. Точки касания делят эти ребра в равных отношениях, считая от вершины S. Найдите объем пирамиды.
касается плоскости основания LMN и боковых ребер пирамиды. Точки касания делят эти ребра в равных отношениях, считая от вершины S. Найдите объем пирамиды.
Физический факультет МГУ, 2004 г.
- Решите уравнение
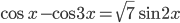 .
. - Решите неравенство
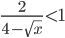 .
. - Решите уравнение
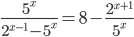 .
. - В правильной треугольной пирамиде отношение бокового ребра к высоте пирамиды равно 2. Найдите отношение радиуса вписанного в пирамиду шара к стороне основания пирамиды.
- Решите неравенство
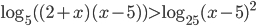 .
. - В параллелограмме ABCD биссектриса тупого угла BAD пересекает сторону CD в точке M такой, что DM : MC = 2 : 1, угол CAM равен
 . Найдите угол BAD.
. Найдите угол BAD. - При каких значениях
 уравнение
уравнение 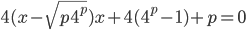 имеет корни и каковы знаки корней при различных значениях
имеет корни и каковы знаки корней при различных значениях  ?
? - Сторона KL прямоугольника KLMN служит высотой конуса с вершиной L, радиус основания этого конуса в три раза длиннее отрезка NK, KL = 6. Шар касается плоскости прямоугольника KLMN в точке M и имеет единственную общую точку с конусом. Найдите радиус шара. Решение
Ответы
2003 г
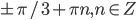
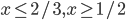
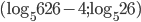
- 2
- x=5, y=1; x=1/3, y=-11/3.
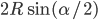
- Если а = 1/2, то x<-2, 1/2<x<1, x>1; если a<-2, то x<a, x>-2; если a = -2, то x<-2, x>-2; в остальных случаях x<-2, x>a.
- 1125/224
2004 г
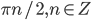
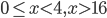
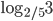
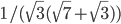
- x<-3, x>5
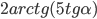
- Корни существуют при p = 0 (только x = 0) и при
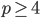 , когда все корни положительны
, когда все корни положительны - 2