Теория чисел
Задачи 61-80

- Число
 при делении на 4 дает в остатке 1, а при делении на 5 дает в остатке 2. Чему равен остаток от деления числа
при делении на 4 дает в остатке 1, а при делении на 5 дает в остатке 2. Чему равен остаток от деления числа  на 20?
на 20? - Докажите, что любая натуральная степень числа 15 при делении на 7 дает остаток 1.
- Докажите, что число
 составное при всех натуральных
составное при всех натуральных  .
. - Докажите, что если одно из чисел
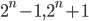 является простым, то второе из них является составным, где
является простым, то второе из них является составным, где  - натуральное число,
- натуральное число, 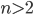 .
. - Найдите все целые числа
 , при которых модуль трехчлена
, при которых модуль трехчлена 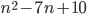 является простым числом.
является простым числом. - Найдите все простые числа
 такие, что
такие, что 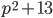 - тоже простое.
- тоже простое. - Числа
 и
и 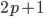 являются простыми и
являются простыми и 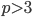 . Докажите, что число
. Докажите, что число 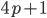 составное.
составное. - Докажите, что число
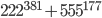 является составным.
является составным. - Найдется ли такое натуральное
 , при котором число
, при котором число 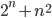 оканчивается на 5?
оканчивается на 5? - Какой цифрой оканчивается число
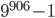 ?
? - Петя и Вася живут в одном доме. На каждом из этажей во всех подъездах дома расположено по 4 квартиры. Петя живет на 5 этаже в квартире 83, а Вася - на 3 этаже в квартире 169. Сколько этажей в их доме?
- В 13-томном справочнике сплошная нумерация страниц. Сколько страниц в одном томе, если в каждом из томов их поровну, а сумма номеров первых и последних страниц равна 39390.
- Расставьте между цифрами 1, 2, 3, 4 и 5 знаки математических действий так, чтобы результатом этих действий было число 20.
- Найдите трехзначное число, равно кубу суммы его цифр.
- Шестая степень натурального числа
 записывается в десятичной системе семью цифрами 2, 4, 5, 8, 8, 9, 9, расположенными в некотором порядке. Найдите
записывается в десятичной системе семью цифрами 2, 4, 5, 8, 8, 9, 9, расположенными в некотором порядке. Найдите  .
. - Известно, что
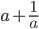 - натуральное число. Докажите, что
- натуральное число. Докажите, что 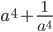 - также натуральное число.
- также натуральное число. - Если все цифры некоторого натурального числа
 переписать в обратном порядке, то новое число будет в 4 раза больше первоначального. Найдите хотя бы одно такое число
переписать в обратном порядке, то новое число будет в 4 раза больше первоначального. Найдите хотя бы одно такое число  .
. - Некоторое натуральное число
 оканчивается на 2. Если двойку перенести с последнего места на первое, то число удвоится. Найдите
оканчивается на 2. Если двойку перенести с последнего места на первое, то число удвоится. Найдите 
- Найдите хотя бы одно натуральное
 , которое делится на 11 без остатка, а при делении на 2, 3, 4, ..., 10 дает в остатке 1.
, которое делится на 11 без остатка, а при делении на 2, 3, 4, ..., 10 дает в остатке 1. - Найдите наименьшее натуральное число, в записи которого задействованы все цифры от 0 до 9, и такого, что оно делится без остатка на 36.