Урок 11. Системы, возникающие из текстовых задач
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
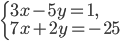
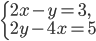
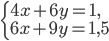
- Для произвольного
 решите систему уравнений
решите систему уравнений 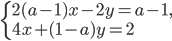
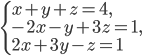
- Известно, что
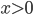 ,
, 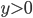 и
и 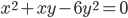 . Найдите
. Найдите 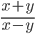 .
. - Найдите все пары
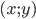 , которые являются решениями уравнения
, которые являются решениями уравнения 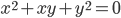 .
. - Известно, что
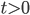 ,
, 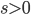 и
и 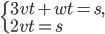 Найдите
Найдите 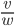 .
. - Известно, что
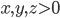 и
и 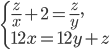 Найдите
Найдите 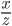 и
и 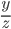 .
. - Известно, что
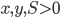 ,
, 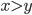 и
и 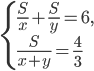 Найдите
Найдите 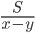 .
. - Известно, что
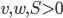 и
и 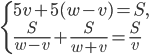 Верно ли, что
Верно ли, что 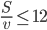 ?
? 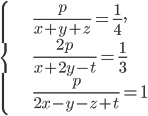 Найдите
Найдите 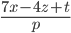 .
.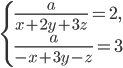 Найдите
Найдите 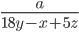 .
.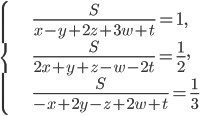 Найдите
Найдите 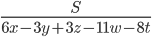 .
.- Известно, что
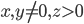 и
и  Найдите
Найдите 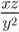 .
. - Найдите
 и
и 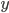 , если
, если 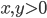 и
и 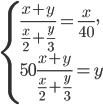
Ответы к домашнему заданию урока 11 из В.В. Ткачук "Математика - абитуриенту"
- (-3; 12)
- нет решений
- (t; (1-4t)/16), t - любое действительное число
- если a = -1, то x=(1-t)/2, y=t, где t - любое действительное число; если а = 3, то x, y - любые; в остальных случаях x=1/2, y=0.
- (3; -1; 2)
- 3
- (0; 0)
- -1
- x/z=1/4, y/z=1/6
- 4
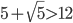
- 11
- 6/17
- -1/6
- -1/5
- x=1080/11, y=1350/11