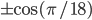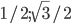Урок 7. [3] Обратные тригонометрические функции
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- Докажите, что
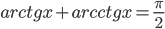 для любых
для любых  .
. - Докажите, что
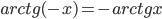 для любых
для любых  .
. - Докажите, что
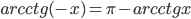 для любых
для любых  .
. - Докажите, что
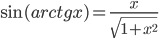 для любых
для любых  .
. - Докажите, что
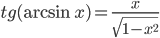 для
для 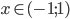 .
. - Докажите, что
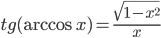 для
для ![x\in [-1;0)\cup (0;1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_159275b161b03bd288aedeeaac885e7d.gif) .
. - Докажите, что
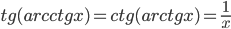 для
для 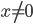 .
. - Докажите, что
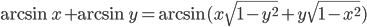 при
при ![x,y\in [0; 1/\sqrt{2}]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_ee1b5f96fa369a6525dcdd02d6a7ceb9.gif)
- Верно ли утверждение предыдущей задачи для любых
![x,y\in [-1;1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_dbc09fcb98dad9a07c96bbf025e105f9.gif) ?
? - Докажите, что
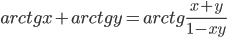 , если
, если  .
. - Верно ли утверждение предыдущей задачи для любых x, y?
- Найдите
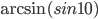 .
. - Найдите
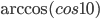 .
. - Найдите
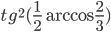 .
. - Найдите
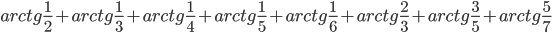 .
. - Решите уравнение
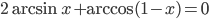 .
. - Решите уравнение
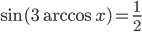 .
. - Решите уравнение
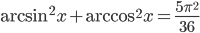 .
.
Ответы к домашнему заданию урока 7 из В.В. Ткачук "Математика - абитуриенту"
- Не верно для x=y=1
- Не верно для x=y=1
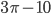
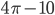
- 1/5
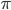
- 0