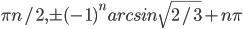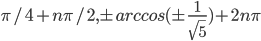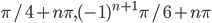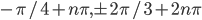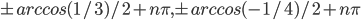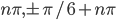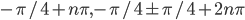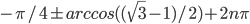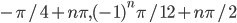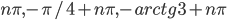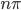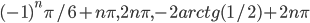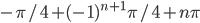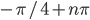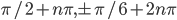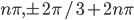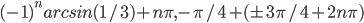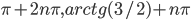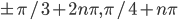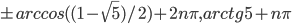Тригонометрия. Урок 2. Группировка и разложение на множители.
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
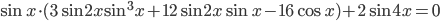
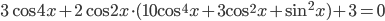
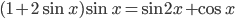
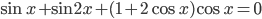
- [3]
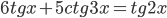
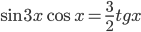
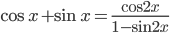
- [3]
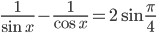
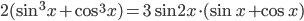
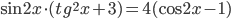
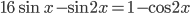
- [3]
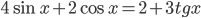
- [2]
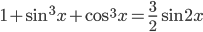
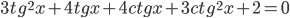
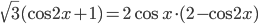
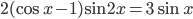
- [3]
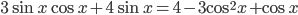
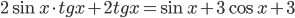
- [2]
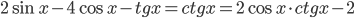
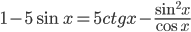
Ответы к домашнему заданию урока 2 из В.В. Ткачук "Математика - абитуриенту"
По умолчанию, 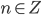 .
.
Тригонометрия. Урок 2. Группировка и разложение на множители.
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
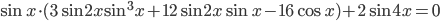
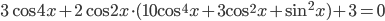
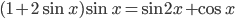
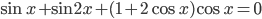
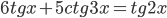
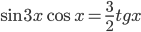
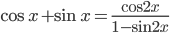
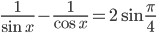
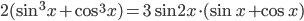
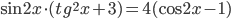
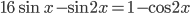
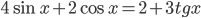
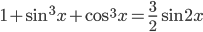
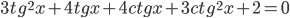
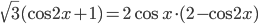
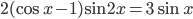
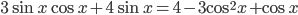
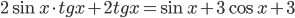
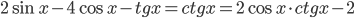
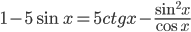
Ответы к домашнему заданию урока 2 из В.В. Ткачук "Математика - абитуриенту"
По умолчанию, 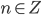 .
.