Урок 24. Касательная
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
- Найти все такие числа
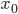 , что касательные к графикам функций
, что касательные к графикам функций 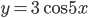 и
и 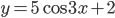 в точках с абсциссой
в точках с абсциссой 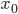 параллельны.
параллельны. - Найти уравнения тех касательных к графику функции
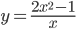 , которые вместе с осями координат ограничивают треугольник площади 1.
, которые вместе с осями координат ограничивают треугольник площади 1. - К параболе
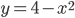 в точке с абсциссой
в точке с абсциссой 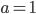 проведена касательная. Найти точку ее пересечения с осью координат.
проведена касательная. Найти точку ее пересечения с осью координат. - Вычислить площадь треугольника, ограниченного осями координат и касательной к графику функции
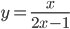 в точке с абсциссой
в точке с абсциссой 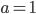 .
. - Найти точки пересечения с осями координат тех касательных к графику функции
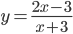 , у которых угловой коэффициент равен 9.
, у которых угловой коэффициент равен 9. - Найти все
 , при которых касательная к графику функции
, при которых касательная к графику функции 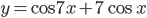 в точке с абсциссой
в точке с абсциссой  параллельна касательной к этому же графику в точке с абсциссой
параллельна касательной к этому же графику в точке с абсциссой 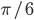 .
. - [3] Найти координаты точки, лежащей на графике функции
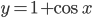 при
при 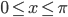 и наименее удаленной от прямой
и наименее удаленной от прямой 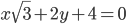 .
. - [2] Прямая касается графика функции
![y=\sqrt[3]{x^2}](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_4b63d449fe81825456b97639e662b5bb.gif) в точке с абсциссой
в точке с абсциссой ![a\in [1/2; 1]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_0ea87a4b0ae32278c1aa84a0fb4cc693.gif) . При каких
. При каких  площадь треугольника, ограниченного этой прямой, осью Ох и прямой х = 2 будет наименьшей? Найти эту наименьшую площадь.
площадь треугольника, ограниченного этой прямой, осью Ох и прямой х = 2 будет наименьшей? Найти эту наименьшую площадь. - Найти координаты точки пересечения касательных к графику функции
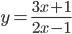 в точках с абсциссами -1 и 3.
в точках с абсциссами -1 и 3. - Проводятся касательные к графику функции
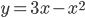 в точке с абсциссой
в точке с абсциссой 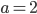 и в точке минимума. Найти площадь треугольника, образованного осью ординат и этими касательными.
и в точке минимума. Найти площадь треугольника, образованного осью ординат и этими касательными. - Найти координаты точки пересечения касательных к графику функции
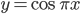 в точках с абсциссами 1/6 и 7/6.
в точках с абсциссами 1/6 и 7/6. - Найти координаты точек пересечения с осью абсцисс касательных к графику функции
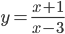 , которые образуют угол 135о с осью Ох.
, которые образуют угол 135о с осью Ох. - Вычислить площадь треугольника, ограниченного осями координат и касательной к графику функции
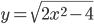 в точке с абсциссой
в точке с абсциссой 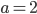 .
. - [2] Прямая касается графика функции
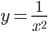 в точке с абсциссой
в точке с абсциссой ![a\in [5;9]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_9e7c589b7d0b02693a6bd3cf32e91cee.gif) . Эта прямая, ось Ох и прямая х = 4 ограничивают треугольник. При каких
. Эта прямая, ось Ох и прямая х = 4 ограничивают треугольник. При каких  его площадь будет наибольшей? Найти эту наибольшую площадь.
его площадь будет наибольшей? Найти эту наибольшую площадь. - [2] На плоскости Оxy рассматриваются прямоугольные треугольники ABC, где угол ACB прямой, А=(2;0), вершина С лежит на отрезке [0;2] оси Ох, а В - на параболе
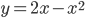 . Какие координаты должна иметь точка В, чтобы площадь треугольника АВС была наибольшей?
. Какие координаты должна иметь точка В, чтобы площадь треугольника АВС была наибольшей?
Ответы к домашнему заданию урока 24 из В.В. Ткачук "Математика - абитуриенту"
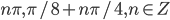
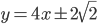
- (0;5)
- 2
- (0;11), (-11/9; 0), (0;47), (-47/9; 0)
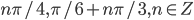
- (0;2)
- a=4/5; наименьшая площадь равна
![48\cdot\sqrt[3]{5/4}/25](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_fbfafaa9d86ca5807ebc98dca45d879a.gif)
- (-7; 4)
- 49/32
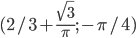
- (0;0), (8;0)
- 1
- a=8, наибольшая площадь равна 1/8
- (2/3; 8/9)