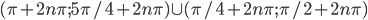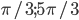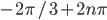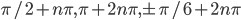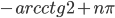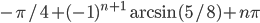Урок 20. Смешанная тригонометрия
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
Задачи 1 - 18 и ответы к ним Задачи 19-35 и ответы к ним
Ответы к домашнему заданию урока 20 из В.В. Ткачук "Математика - абитуриенту"
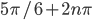
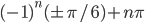
![{3/2}\cup [-\pi/3+n\pi; -\pi/4+n\pi)\cup (\pi/4+n\pi; \pi/3+n\pi], n=1,2,\ldots](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_c0f82f989ed13a7d33fc7fd82cde5531.gif)
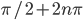
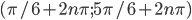
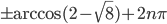
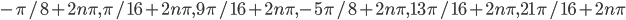
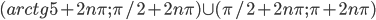
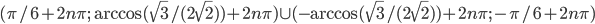
![(\pi/4+n\pi; \pi/3+n\pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a45ddae2db22dbcceb2f2c9911c7f2cb.gif)
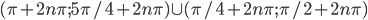
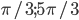
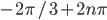
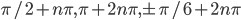
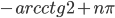
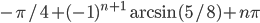
- нет решений
Урок 20. Смешанная тригонометрия
Домашнее задание из В.В. Ткачук "Математика - абитуриенту"
Задачи 1 - 18 и ответы к ним Задачи 19-35 и ответы к ним
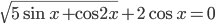
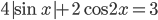
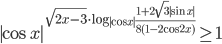
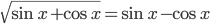
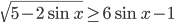
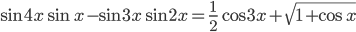
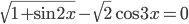
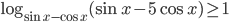
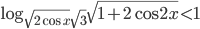
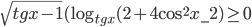
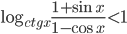
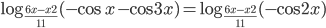
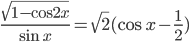
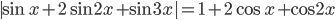
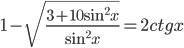
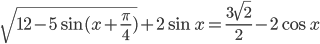
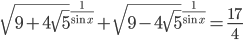
Ответы к домашнему заданию урока 20 из В.В. Ткачук "Математика - абитуриенту"
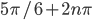
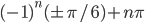
![{3/2}\cup [-\pi/3+n\pi; -\pi/4+n\pi)\cup (\pi/4+n\pi; \pi/3+n\pi], n=1,2,\ldots](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_c0f82f989ed13a7d33fc7fd82cde5531.gif)
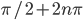
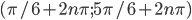
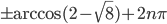
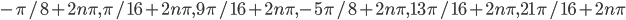
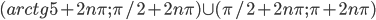
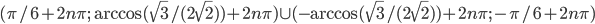
![(\pi/4+n\pi; \pi/3+n\pi]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_a45ddae2db22dbcceb2f2c9911c7f2cb.gif)