Урок 15. Текстовые задачи. Смеси

Домашнее задание из В.В. Ткачук "Математика - абитуриенту"

1. От двух однородных кусков сплава с различным процентным содержанием меди, весящих соответственно m и n кг, отрезано по куску равного веса. Каждый из отрезанных кусков был сплавлен с остатком другого куска, после чего процентное содержание меди в получившихся сплавах стало одинаковым. Сколько весил каждый из отрезанных кусков?
2. [3] В сосуд с чистой водой налили 6 литров 64%-ного (по объему) раствора спирта, а затем после полного перемешивания вылили равное количество (т.е. 6 литров) получившегося раствора. Сколько воды было первоначально в сосуде, если после троекратного повторения этой операции в сосуде получился 37%-ный раствор спирта?
3.  В баке находится 100 литров смеси кислоты с водой. Из бака отлили часть смеси и добавили равное по объему количество воды, которое на 10 литров превышает первоначальное количество кислоты в смеси.  Затем снова отлили такое же количество смеси, как в первый раз, в результате чего количество кислоты в баке уменьшилось в 4 раза по сравнению с количеством ее в исходной смеси. Определить количество воды в исходной смеси.
4. [3] В двух различных емкостях содержались смеси воды и песка, причем в первой емкости было 1000 кг смеси, а во второй – 1960 кг. В обе емкости добавили воды. При этом процентное содержание песка в смесях уменьшилось в k раз в первой емкости и в p раз во второй. О числах k иp известно только, что kp=9-k. Найти наименьшее количество воды, которое могло быть долито в обе емкости вместе.
5. Свежие фрукты содержат 72% воды, а сухие – 20%. Сколько сухих фруктов получится из 20 кг свежих фруктов?
6. Имеются два слитка золота с серебром. Процентное содержание золота в первом слитке в два с половиной раза больше, чем процентное содержание золота во втором слитке. Если сплавить оба слитка вместе, то получится слиток, в котором будет 40% золота. Найти, во сколько раз первый слиток тяжелее второго, если известно, что при сплавке равных по весу частей первого и второго слитков получается сплав, в котором 35% золота.
7. Имеются два раствора серной кислоты в воде, первый – 40% -ный, второй – 60%-ный. Эти два раствора смешали, после чего добавили 5 кг чистой воды и получили 20%-ный раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-ного раствора, то получился бы 70%-ный раствор. Сколько было 40%-ного и 60%-ного растворов?
8.  Сплавляя два одинаковых по весу куска чугуна с разным содержанием хрома, получили сплав, в котором 12 кг хрома. Если бы первый кусок был в два раза тяжелее, то в сплаве содержалось бы 16 кг хрома. Известно, что содержание хрома в первом куске на 5% меньше, чем во втором. Найти процентное содержание хрома в каждом из кусков.
9. Для приготовления смеси из двух жидкостей А и В было взято 16 литров жидкости А и разлито в два сосуда объемом по 16 литров каждый. Затем первый сосуд был долит жидкостью В и произведено перемешивание. Полученной смесью был дополнен сверху второй сосуд. Если отлить из второго сосуда в первый 8 литров получившийся смеси, то в первом сосуде будет жидкости А на три литра больше, чем во втором. Сколько всего использовано жидкости В для приготовления смеси?
10. Имеются два бака. Первый наполнен чистым глицерином, второй – водой. Взяли два трехлитровых ковша, зачерпнули первым полным ковшом глицерин из первого бака, а вторым полным ковшом зачерпнули воду из второго бака. После этого содержимое первого ковша влили во второй бак, а содержимое второго ковша – в первый. После перемешивания эту процедуру повторили. В результате половину объема первого бака занял чистый глицерин. Найти объемы баков, если известно, что их суммарный объем в 10 раз больше объема первого бака.
11. Имеются два сплава, состоящих из цинка, меди и олова. Первый сплав содержит 40% олова, второй – 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько кг олова в новом сплаве?
12. [2] Имеются три сплава. Первый сплав содержит 60% алюминия, 15% меди и 25% магния; второй – 30% меди и 70% магния; третий – 45% алюминия и 55% магния. Из них необходимо приготовить новый сплав, содержащий 20% меди. Какое наименьшее и какое наибольшее процентное содержание алюминия может быть в этом новом сплаве?
13.  Имеются два раствора одной и той же соли в воде.  Для получения смеси, содержащей 10 г соли и 90 г воды, берут первого раствора по весу вдвое больше, чем второго. Через неделю из каждого килограмма первого и второго растворов испарилось по 200 г воды, и для получения такой же смеси, как и раньше, требуется первого раствора уже вчетверо больше по весу, чем второго. Сколько г соли содержалось первоначально в 100 г каждого раствора?
14. Имеются два слитка сплавов меди и олова. Первый весит 3 кг и содержит 40% меди, второй весит 7 кг и содержит 30% меди. Какого веса нужно взять куски этих слитков, чтобы после их переплавки получить 8 кг сплава, содержащего r% меди? При каких r задача имеет решение?
15. Имеются три слитка золота с серебром. Известно, что количество золота в 2 г сплава из третьего слитка то же самое, что во взятых вместе 1 г сплава из первого слитка и 1 г сплава из второго слитка. Вес третьего слитка равен суммарному весу части первого слитка, содержащей 10 г золота и части второго слитка, содержащей 80 г золота. Третий слиток в четыре раза тяжелее первого и содержит    75 г золота. Сколько золота содержит первый слиток?
16. [2] Даны две смеси, состоящие из одних и тех же веществ А, Б, В, но взятых в различных весовых соотношениях. В первой смеси вещества А в два раза меньше, чем вещества Б, и в три раза меньше, чем вещества В. Во второй смеси вещества Б в три раза меньше, чем вещества А, и в два раза меньше, чем вещества В. Сколько следует взять каждой смеси и сколько добавить вещества Б, чтобы получить 7 кг новой смеси, в которой вещества А в три раза меньше, чем вещества Б и в два раза меньше, чем вещества В?
17. Есть два слитка – сплавы цинка с медью. Вес первого – 2 кг, второго – 3 кг.  Эти два слитка сплавили вместе с 5 кг сплава цинка с медью, в котором цинка было 45%, и получили сплав, в котором цинка стало 50%. Если бы процентное содержание цинка в первом слитке было равно процентному содержанию цинка во втором, а процентное содержание цинка во втором было такое же, как в первом (то есть их процентные содержания поменялись), то сплавив эти два слитка с 5 кг сплава, в котором содержится 60% цинка, получили бы сплав, в котором цинка содержится 55%. Найти процентное содержание цинка в первом и во втором слитках.
18. В пустой резервуар по двум трубам одновременно начинают поступать чистая вода и раствор кислоты постоянной концентрации. После наполнения резервуара в нем получился 5% раствор кислоты. Если бы в тот момент, когда резервуар был наполнен наполовину, подачу воды прекратили, то после наполнения резервуара получили бы 10%-ный раствор кислоты. Определить, какая труба и во сколько раз подаёт раствор быстрее.
19. Две трубы, работая вместе, подают в бак 100 литров жидкости в минуту. Имеются два раствора кислоты – сильный и слабый. Если смешать по 10 литров каждого раствора и 20 л воды, то получится 40 литров 20%-ного раствора. Известно также, что если в течение часа подавать в первоначально пустой бак по первой трубе слабый раствор, а по второй – сильный, то получится 30%-ный раствор кислоты. Какой концентрации ( в процентах) получится кислота, если в течение часа первоначально подавать в пустой бак по первой трубе сильный, а по второй трубе – слабый растворы? (Считать, что при смешивании воды и кислоты объем не меняется)

Ответы к домашнему заданию урока 15 из В.В. Ткачук "Математика - абитуриенту"

1. mn/(m+n) кг
2. 18 л
3. 60 л
4. 3480 кг
5. 7 кг
6. первый в 2 раза тяжелее второго слитка
7. 40% - 1 кг и 60% - 2 кг
8. 5%, 10%
9. 4 л
10. 10 л и 90 л
11. 170 кг
12. 15% и 40%
13. 5 г и 20 г
14. 0,8r-24; 32-0,8r,  $31,25\leq r\leq 33,75$
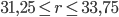
15. 12,5 г
16. 4 кг 1-й смеси, 1 кг 2-й смеси и 2 кг вещества Б
17. 40% и 65%
18. первая труба в два раза быстрее
19. 50%