



 Найдите все значения переменной, при которых разность дробей
Найдите все значения переменной, при которых разность дробей  и
и  равна дроби
равна дроби  .
.
















 Пусть
Пусть 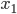 и
и 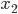 - корни уравнения
- корни уравнения  . Найдите значение выражения
. Найдите значение выражения 
Ответы
- -3


- 1/6;1
- 0;5
- -11
- -1/6;0
- 2
- -3
- -5
- 10/3

- 29/19
- -3;3

- -5;-4;1;2
- -3;4
- 0
- -3;4
- 6
- -3
- 2
- -199/60




 Найдите все значения переменной, при которых разность дробей
Найдите все значения переменной, при которых разность дробей  и
и  равна дроби
равна дроби  .
.
















 Пусть
Пусть 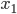 и
и 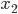 - корни уравнения
- корни уравнения  . Найдите значение выражения
. Найдите значение выражения 
Ответы



