Решение пробного ЕГЭ 2015 по математике (март) Профильный уровень 11 класс
- Для покраски 67 кв. м необходимо
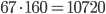 г краски. Это
г краски. Это 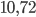 кг. Значит, количество банок необходимо
кг. Значит, количество банок необходимо 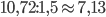 . Но так как количество банок должно быть целым числом, то округляем, причем в большую сторону, так как округление в меньшую сторону означает, что краски на весь потолок не хватит. Значит, 8 банок.
. Но так как количество банок должно быть целым числом, то округляем, причем в большую сторону, так как округление в меньшую сторону означает, что краски на весь потолок не хватит. Значит, 8 банок. - Одна клетка вдоль оси ординат (это вертикаль) значит 4 г. За первые три минуту функция изменила значение на 3 клетки, что соответствует 12 г. То есть 12 г вступило в реакцию за первые три минуты.
- Для каменного фундамента необходимо
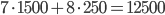 р. Для бетонного необходимо
р. Для бетонного необходимо 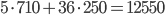 р. Дешевле будет стоить каменный фундамент.
р. Дешевле будет стоить каменный фундамент. - Похожая задача разбирается здесь (номер B5). Обрамим треугольник прямоугольником так, что все вершины треугольника принадлежат сторонам прямоугольника, а одна вершина еще и совпадает с вершиной прямоугольника. Такой прямоугольник состоит из исходного закрашенного треугольника и еще трех прямоугольных незакрашенных треугольников. Площадь закрашенного можно найти как разность площади прямоугольника и суммы площадей трех незакрашенных:
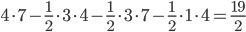
- Вероятность того, что чайник выйдет из строя в течение первых пяти лет равна
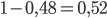 . И это вероятность равна сумме вероятностей двух несовместных событий: чайник вышел из строя в течение первых двух лет работы и чайник вышел из строя в течение следующих трех лет работы. Тогда
. И это вероятность равна сумме вероятностей двух несовместных событий: чайник вышел из строя в течение первых двух лет работы и чайник вышел из строя в течение следующих трех лет работы. Тогда 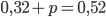 , откуда
, откуда 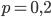 .
. - Так как
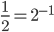 и
и 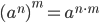 , то уравнение принимает вид
, то уравнение принимает вид  , то есть
, то есть 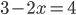 и
и 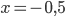 .
. - Синус угла А равен
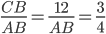 , откуда
, откуда 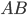 равно 16. Так как
равно 16. Так как 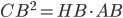 (по метрическим соотношениям в прямоугольном треугольнике), то
(по метрическим соотношениям в прямоугольном треугольнике), то 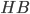 равно
равно 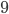 . Значит,
. Значит, 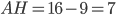 . Кстати, при нахождении каких-либо элементов треугольника себя всегда можно проверить здесь.
. Кстати, при нахождении каких-либо элементов треугольника себя всегда можно проверить здесь. - Если производная положительна на каком-либо интервале, то соответствующая функция на этом интервале возрастает. Поэтому на [-7; -3]
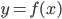 возрастает, хотя производная то убывает, то возрастает. А важен только знак производной - и она положительна. Получается, что функция начинает движение с точки
возрастает, хотя производная то убывает, то возрастает. А важен только знак производной - и она положительна. Получается, что функция начинает движение с точки 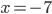 и далее все время возрастает. Значит, наименьшее значение в точке
и далее все время возрастает. Значит, наименьшее значение в точке 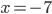 . Здесь в решении для простоты объяснения допущены некоторые вольности в фразах.
. Здесь в решении для простоты объяснения допущены некоторые вольности в фразах. - Многогранник
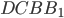 является треугольной пирамидой с основанием
является треугольной пирамидой с основанием 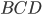 и высотой
и высотой 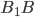 . Поэтому его объем равен
. Поэтому его объем равен 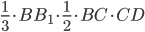
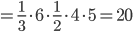 .
. - В решении нам пригодятся формулы приведения и формула для синуса двойного угла. Заметим, что
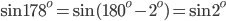 и
и 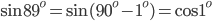 . Тогда выражение принимает вид
. Тогда выражение принимает вид 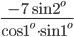 . Домножим числитель и знаменатель дроби на
. Домножим числитель и знаменатель дроби на 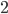 и тогда к знаменателю применима формула для синуса двойного угла. После сокращения получаем
и тогда к знаменателю применима формула для синуса двойного угла. После сокращения получаем 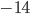 .
.
- Поставим известные данные в формулу
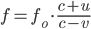 . Получим
. Получим 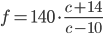 . И перейдем к неравенству
. И перейдем к неравенству 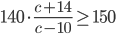 , которое решим методом интервалов. Перенесем
, которое решим методом интервалов. Перенесем 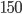 в левую часть, приведем к общему знаменателю дроби и получим в итоге, что
в левую часть, приведем к общему знаменателю дроби и получим в итоге, что 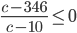 . Откуда
. Откуда ![c\in (10; 346]](http://www.itmathrepetitor.ru/wp-content/plugins/latex/cache/tex_92c469130a301bc10ba37e4da598ca37.gif) и наибольшее значение
и наибольшее значение  равно
равно 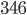 .
. - Вспомним две формулы: объем шара равен
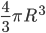 и объем конуса равен
и объем конуса равен 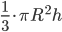 . Но в данном конусе высота равна радиусу
. Но в данном конусе высота равна радиусу 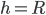 шара, так как центр шара совпадает с центром основания конуса. Значит,
шара, так как центр шара совпадает с центром основания конуса. Значит, 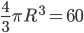 , откуда
, откуда 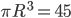 . И объем конуса равен
. И объем конуса равен 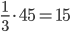 .
. - Производительность первого переводчика равна
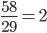 стр/день, второго -
стр/день, второго - 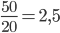 стр/день. Если первый возьмет себе
стр/день. Если первый возьмет себе  страниц, то второму останется
страниц, то второму останется 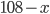 стр. Так как время работы каждого переводчика одинаково, то
стр. Так как время работы каждого переводчика одинаково, то 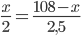 , откуда
, откуда  . Значит, первый переводчик должен взять себе на
. Значит, первый переводчик должен взять себе на 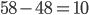 стр меньше.
стр меньше. - Производная функции равна
 . Приравниваем ее к нулю и решаем уравнение:
. Приравниваем ее к нулю и решаем уравнение: 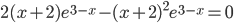
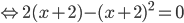 (сократили на положительное выражение
(сократили на положительное выражение 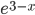 без потери корней). Тогда
без потери корней). Тогда 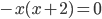 , откуда
, откуда 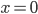 или
или 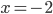 . Производная меняет знак с "+" на "-" только в точке
. Производная меняет знак с "+" на "-" только в точке 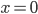 .
. - а) Возведем правую и левую части уравнения в квадрат. Однако, данное преобразование может привести к появлению посторонних корней. Поэтому дополнительно требуем, чтобы
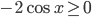 . Получаем уравнение
. Получаем уравнение 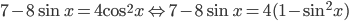
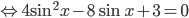 . Здесь полезно повторить тригонометрические формулы. Решаем данное уравнение как квадратное относительно
. Здесь полезно повторить тригонометрические формулы. Решаем данное уравнение как квадратное относительно 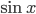 . Тогда
. Тогда 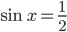 . (второй корень
. (второй корень 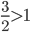 ). Так как
). Так как  должен быть неположительным, то
должен быть неположительным, то 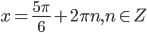 .
.
б) Решим двойное неравенство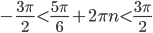
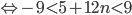
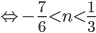 . Так как
. Так как 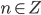 , то есть целое число, то
, то есть целое число, то 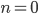 или
или 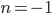 . Подставляем данные значения в формулу
. Подставляем данные значения в формулу 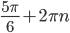 и находим два конкретных угла.
и находим два конкретных угла. - Проведем через точку М прямую, параллельную AD, до пересечения в точке К с прямой SB. Точка К существует, так как прямая AD параллельна плоскости BSC. Тогда ADMK - искомое сечение. В равнобедренном треугольнике SDC известны все стороны, поэтому медиану DM без труда можно найти по формуле
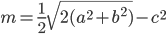 (подробнее смотрите справочник). Медиана равна
(подробнее смотрите справочник). Медиана равна 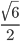 . При нахождении каких-либо элементов треугольника себя всегда можно проверить здесь. Тогда в трапеции ADMK известны боковые стороны DM=AK и нижнее основание AD. Верхнее основание KM равно
. При нахождении каких-либо элементов треугольника себя всегда можно проверить здесь. Тогда в трапеции ADMK известны боковые стороны DM=AK и нижнее основание AD. Верхнее основание KM равно  , так как KM - средняя линия треугольника SBC. Осталось найти площадь равнобедренной трапеции, если известны все стороны. Для этого можно из точек K и M провести две высоты KH и MT на AD. Тогда TD равно
, так как KM - средняя линия треугольника SBC. Осталось найти площадь равнобедренной трапеции, если известны все стороны. Для этого можно из точек K и M провести две высоты KH и MT на AD. Тогда TD равно  . И после нахождения высоты по теореме Пифагора в треугольнике MTD применить формулу площади трапеции
. И после нахождения высоты по теореме Пифагора в треугольнике MTD применить формулу площади трапеции 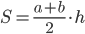 .
. - В этом примере полезно вспомнить, что
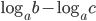 можно заменить на эквивалентное по знаку выражение
можно заменить на эквивалентное по знаку выражение 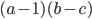 (и учесть область определения логарифмов, конечно же). Повторить свойства логарифмов. Этот факт пригодится в конце решения. А пока упростим все слагаемые (и помним, что при преобразованиях меняются ограничения на
(и учесть область определения логарифмов, конечно же). Повторить свойства логарифмов. Этот факт пригодится в конце решения. А пока упростим все слагаемые (и помним, что при преобразованиях меняются ограничения на  , которые проверим в конце решения):
, которые проверим в конце решения): 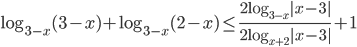 . Так как
. Так как 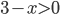 из-за существования логарифма в левой части, то
из-за существования логарифма в левой части, то 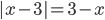 и неравенство принимает вид
и неравенство принимает вид 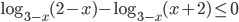
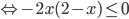 . Откуда с учетом ограничений исходного неравенства получаем ответ. Самое важное: не забыть модуль, когда выносим четную степень; не забыть, что свойство
. Откуда с учетом ограничений исходного неравенства получаем ответ. Самое важное: не забыть модуль, когда выносим четную степень; не забыть, что свойство 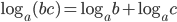 применимо только при
применимо только при 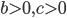 . Поэтому при разложении левой части в начале решения разложение квадратного трехчлена именно такое
. Поэтому при разложении левой части в начале решения разложение квадратного трехчлена именно такое 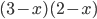 , а не
, а не 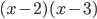 .
. - Если
 - сумма в рублях, которую Васильев каждый год вкладывает в банк, то
- сумма в рублях, которую Васильев каждый год вкладывает в банк, то 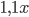 - сумма через год,
- сумма через год, 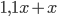 - новый вклад через год,
- новый вклад через год, 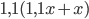 - сумма через два года и так далее. Приходим к равенству
- сумма через два года и так далее. Приходим к равенству 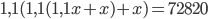 . Решив это линейное уравнение, получим
. Решив это линейное уравнение, получим 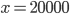 .
. - Когда-то давно задачи такого типа часто встречались на вступительных экзаменах в МФТИ. И это радует. Каждую пару
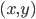 можно рассматривать как точку на плоскости в заданной системе координат. Тогда система уравнений - это точки пересечения графиков уравнений. Второе уравнение системы
можно рассматривать как точку на плоскости в заданной системе координат. Тогда система уравнений - это точки пересечения графиков уравнений. Второе уравнение системы 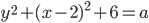 является уравнением окружности, если
является уравнением окружности, если 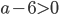 . Тогда ее центр находится в точке
. Тогда ее центр находится в точке 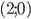 , а радиус равен
, а радиус равен 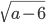 . Так как
. Так как  - параметр, то данная окружность имеет фиксированный центр и произвольный радиус, который мы можем регулировать параметром. Необходимо подобрать такой параметр, чтобы окружность пересекла график первого уравнения только в одной точке. Первое уравнение преобразуем к виду
- параметр, то данная окружность имеет фиксированный центр и произвольный радиус, который мы можем регулировать параметром. Необходимо подобрать такой параметр, чтобы окружность пересекла график первого уравнения только в одной точке. Первое уравнение преобразуем к виду 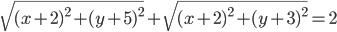 . Если вспомнить, что расстояние между двумя точками на плоскости может быть найдено по формуле
. Если вспомнить, что расстояние между двумя точками на плоскости может быть найдено по формуле 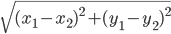 , то становится понятно, почему первое уравнение геометрически означает, что сумма расстояния от точки
, то становится понятно, почему первое уравнение геометрически означает, что сумма расстояния от точки 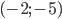 до точки
до точки 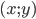 и расстояния от точки
и расстояния от точки 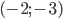 до точки
до точки 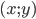 равна
равна 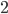 . Но расстояние между точками
. Но расстояние между точками 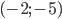 и
и 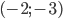 равно 2, поэтому точка
равно 2, поэтому точка 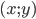 может быть только на отрезке между этими двумя точками. То есть графиком первого уравнения является отрезок. Осталось выбрать такое
может быть только на отрезке между этими двумя точками. То есть графиком первого уравнения является отрезок. Осталось выбрать такое  , чтобы окружность пересекла отрезок ровно в одной точке.
, чтобы окружность пересекла отрезок ровно в одной точке. - а) Довольно быстро строится пример:
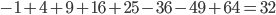 . Вопрос только в фразе "Между ними произвольным образом расставляют знаки", то есть первое число
. Вопрос только в фразе "Между ними произвольным образом расставляют знаки", то есть первое число 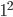 не может стать
не может стать 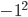 . Поэтому такой пример, строго говоря, недопустим. Но, наверное, это замечание не стоит учитывать. б) Заметим, что
. Поэтому такой пример, строго говоря, недопустим. Но, наверное, это замечание не стоит учитывать. б) Заметим, что 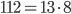 . Следовательно, можно изучить серии чисел из восьмерок. Если окажется, что в разбиении на восьмерки числа
. Следовательно, можно изучить серии чисел из восьмерок. Если окажется, что в разбиении на восьмерки числа 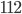 каждая восьмерка чисел может давать в сумме ноль, то решение найдено. Действительно, такое разбиение существует (это восьмерки последовательных чисел) и знаки в каждой из них можно выбрать такие: +, -, -, +, -, +, +, -. в) Рассмотреть остаток от деления на 4.
каждая восьмерка чисел может давать в сумме ноль, то решение найдено. Действительно, такое разбиение существует (это восьмерки последовательных чисел) и знаки в каждой из них можно выбрать такие: +, -, -, +, -, +, +, -. в) Рассмотреть остаток от деления на 4.
смотрите еще Досрочный ЕГЭ март, 2015 по математике с ответами и решениями

В 6 задании
спасибо, в ответах правильно, здесь же опечатка