Вариант вступительных экзаменов по математике в Московский технический университет связи и информатики
МТУСИ, 1997 г.
- Решите уравнение
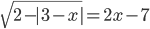
- Решите неравенство
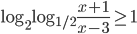
- Докажите тождество
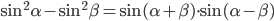
- Найдите целочисленные решения системы уравнений
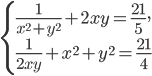 .
. - При каких
 уравнение
уравнение 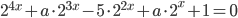 имеет единственное решение? Найдите это решение.
имеет единственное решение? Найдите это решение. - Найдите расстояние между прямыми, заданными уравнениями
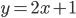 и
и 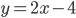 .
. - При каких положительных
 числа
числа 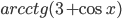 и
и 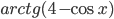 являются величинами двух углов некоторого прямоугольного треугольника?
являются величинами двух углов некоторого прямоугольного треугольника? - Решите уравнение
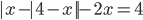
- Двум рабочим было поручено изготовить партию одинаковых деталей. После того, как первый проработал 2 ч, а второй 5 ч, оказалось, что они выполнили половину всей работы. Проработав совместно еще 3 часа, они установили, что им осталось выполнить 0,05 всей работы. За какой промежуток времени каждый из них, работая отдельно, может выполнить всю работу?
- Решите неравенство
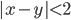 и дайте геометрическую интерпретацию.
и дайте геометрическую интерпретацию.
Ответы
- 4
- [-7/3; -1)
- (2; 1), (1;2), (-2;-1), (-1;-2)
- a = 3/2; x=0
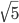
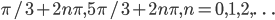
- 0
- 12 ч и 15 ч