Как решать квадратные уравнения

Алгоритм решения квадратного уравнения
Речь идет о поиске только действительных корней квадратного уравнения.
Шаг 1: Записываем уравнение в стандартном виде
В общем виде квадратное уравнение можно записать так:
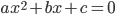
Здесь  - любое ненулевое число,
- любое ненулевое число, 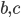 - любые числа, a
- любые числа, a  - то число, которое необходимо найти. Такой вид уравнения называют стандартным. Например,
- то число, которое необходимо найти. Такой вид уравнения называют стандартным. Например, 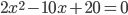 - квадратное уравнение в стандартном виде, причем
- квадратное уравнение в стандартном виде, причем 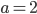 ,
, 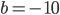 и
и 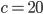 . Число
. Число  называют старшим коэффициентом, число
называют старшим коэффициентом, число  - свободным коэффициентом. А все выражение вида
- свободным коэффициентом. А все выражение вида 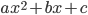 называют квадратным трехчленом.
называют квадратным трехчленом.
Типичная ошибка: считать, что 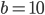 , то есть забыть про знак "-".
, то есть забыть про знак "-".
Cтоит заметить, что все коэффициенты уравнения 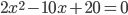 можно уменьшить в
можно уменьшить в 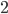 раза. Уравнение примет вид
раза. Уравнение примет вид 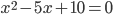 . Числа
. Числа  ,
,  и
и  , естественно, изменились (уменьшились!). Зато корни уравнения остались прежними. Поэтому всегда стоит проверять, а нельзя ли таким образом упростить уравнение, чтобы легче было далее находить корни.
, естественно, изменились (уменьшились!). Зато корни уравнения остались прежними. Поэтому всегда стоит проверять, а нельзя ли таким образом упростить уравнение, чтобы легче было далее находить корни.
Итак, первым делом необходимо привести квадратное уравнение к стандартному виду. Для этого можно раскрывать скобки, приводить подобные слагаемые, переносить слагаемые из одной части уравнения в другую (при этом слагаемые меняют знак). Например, 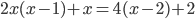 . Раскрываем скобки:
. Раскрываем скобки: 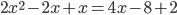 . Приводим подобные слагаемые:
. Приводим подобные слагаемые: 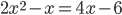 . Переносим все слагаемые из правой части в левую:
. Переносим все слагаемые из правой части в левую: 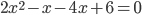 (повторю: такие слагаемые меняют свой знак). И опять приводим подобные слагаемые:
(повторю: такие слагаемые меняют свой знак). И опять приводим подобные слагаемые: 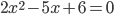 . Получим квадратное уравнение в стандартном виде. Причем
. Получим квадратное уравнение в стандартном виде. Причем 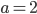 ,
, 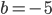 и
и 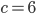 .
.
Типичная ошибка: забыть поменять знак слагаемого при переносе.
Типичная ошибка: перепутать слагаемые местами и неправильно определить коэффициенты. Например, 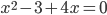 . И кажется, что
. И кажется, что 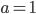 ,
, 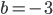 и
и 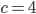 . На самом деле,
. На самом деле, 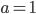 ,
, 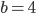 и
и 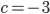 .
.
Интересный случай: предположим, что получилось уравнение 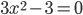 . Чему равно
. Чему равно  ? На этот вопрос не каждый может ответить уверенно. Ответ:
? На этот вопрос не каждый может ответить уверенно. Ответ: 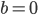 .
.
Интересный случай: дано уравнение 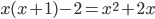 . Мы смело раскрываем скобки и переносим
. Мы смело раскрываем скобки и переносим 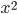 и
и 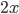 из правой части в левую. Но после приведения подобных слагаемых получается уравнение
из правой части в левую. Но после приведения подобных слагаемых получается уравнение 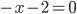 . Нет
. Нет 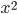 ! Ни о каком стандартном виде квадратного уравнения здесь не может быть и речи просто потому, что это не квадратное уравнение, а совсем другая история под названием "Линейное уравнение".
! Ни о каком стандартном виде квадратного уравнения здесь не может быть и речи просто потому, что это не квадратное уравнение, а совсем другая история под названием "Линейное уравнение".
Замечание: опытные в квадратных уравнениях математики советуют всегда делать коэффициент  положительным. Для этого левую и правую части уравнения всегда можно домножить на
положительным. Для этого левую и правую части уравнения всегда можно домножить на 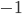 . Например,
. Например, 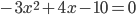 заменим на
заменим на 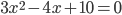 . По-простому говоря, каждое слагаемое меняет знак. Да, это другое уравнение и коэффициенты другие. Но корни у него такие же, как и у исходного уравнения. Поэтому далее спокойно можно работать с новым. Зачем делать
. По-простому говоря, каждое слагаемое меняет знак. Да, это другое уравнение и коэффициенты другие. Но корни у него такие же, как и у исходного уравнения. Поэтому далее спокойно можно работать с новым. Зачем делать  положительным? Например, затем, чтобы было меньше арифметических ошибок, когда будем находить дискриминант. Что такое дискриминант, узнаем в следующем шаге.
положительным? Например, затем, чтобы было меньше арифметических ошибок, когда будем находить дискриминант. Что такое дискриминант, узнаем в следующем шаге.
Шаг 2: Находим дискриминант.
У нас есть квадратное уравнение в виде 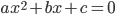 . Вычисляем число
. Вычисляем число 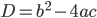 , которое называется дискриминантом квадратного уравнения. Например, для уравнения
, которое называется дискриминантом квадратного уравнения. Например, для уравнения 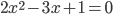 дискриминант равен
дискриминант равен 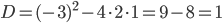 .
.
Типичная ошибка: часто вместо 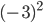 пишут
пишут 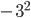 , то есть забывают скобки, но это уже
, то есть забывают скобки, но это уже 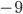 , а не
, а не 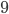 .
.
Типичная ошибка: неправильно определяют коэффициенты  ,
,  и
и 
Типичная ошибка: в слагаемом 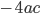 неправильно определяют окончательный знак. Например, в
неправильно определяют окончательный знак. Например, в 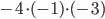 все-таки в итоге получается
все-таки в итоге получается 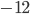 , а не
, а не 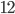 .
.
Редкая ошибка: дискриминант пишут с большой буквы, видимо, из уважения или считая, что это фамилия.
Шаг 3: Находим корни уравнения
У нас есть дискриминант 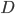 . Далее все зависит от его знака.
. Далее все зависит от его знака.
Если 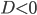 , то корней у уравнения нет. Ответ: корней нет. Вот так внезапно решение закончилось. Например, в уравнении
, то корней у уравнения нет. Ответ: корней нет. Вот так внезапно решение закончилось. Например, в уравнении 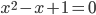 дискриминант равен
дискриминант равен 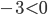 . Поэтому корней нет. Кстати, что это значит? Это значит, что какое бы число вы не выбрали, подстановка его в выражение
. Поэтому корней нет. Кстати, что это значит? Это значит, что какое бы число вы не выбрали, подстановка его в выражение 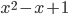 вместо
вместо  никогда не даст
никогда не даст 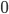 . Проверим число
. Проверим число 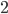 , например:
, например: 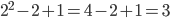 . Не ноль. То есть
. Не ноль. То есть 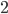 - не корень. Аналогично с любым другим числом: ноль никогда не получится.
- не корень. Аналогично с любым другим числом: ноль никогда не получится.
Если 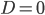 , то
, то 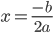 . Числа
. Числа  и
и  - это как раз те коэффициенты из стандартной записи уравнения. Например, в уравнении
- это как раз те коэффициенты из стандартной записи уравнения. Например, в уравнении 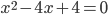 дискриминант
дискриминант 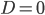 . Тогда
. Тогда 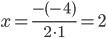 . Ответ:
. Ответ: 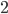 .
.
Типичная ошибка: неправильно подставляют  в формулу
в формулу 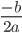 . Ошибаются со знаком. Ведь если
. Ошибаются со знаком. Ведь если 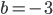 , например, то
, например, то 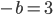 .
.
Если 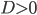 . То в ответе будет два корня, которые можно найти по формулам
. То в ответе будет два корня, которые можно найти по формулам 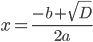 и
и 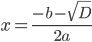 . Например, в уравнении
. Например, в уравнении 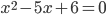 дискриминант
дискриминант 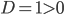 . Тогда
. Тогда 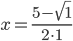 и
и 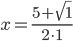 . Так как
. Так как 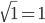 , то
, то 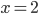 и
и 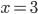 . Ответ:
. Ответ: 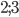 .
.
Замечание: часто для сокращения пишут две формулы в одной: 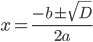 .
.
Замечание: иногда дискриминант может оказаться "некрасивым", например, 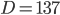 . Такое может быть, и терять самообладание не стоит. Совет один: перепроверить решение и, если ошибка не найдена, со спокойной совестью решать дальше. Чаще всего задачи придумывают так, чтобы дискриминант были полным квадратом (кстати, полезно выучить таблицу квадратов чисел от 1 до 20). Но иногда попадаются ответы вида
. Такое может быть, и терять самообладание не стоит. Совет один: перепроверить решение и, если ошибка не найдена, со спокойной совестью решать дальше. Чаще всего задачи придумывают так, чтобы дискриминант были полным квадратом (кстати, полезно выучить таблицу квадратов чисел от 1 до 20). Но иногда попадаются ответы вида 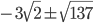 .
.
Типичная ошибка: неправильно находят 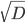 . Например, считают, что
. Например, считают, что 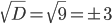 . На самом деле,
. На самом деле, 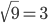 . Отрицательным выражение
. Отрицательным выражение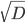 быть не может (по определению арифметического квадратного корня).
быть не может (по определению арифметического квадратного корня).
Вот и весь алгоритм. Конечно, есть еще много деталей. Например, есть неполные квадратные уравнения, когда лучше решать способами без дискриминанта. Есть еще уравнения, сводящиеся к квадратным. Есть еще поиск комплексных корней квадратного уравнения (для ЕГЭ это излишне). Кстати, проверить свое решение квадратного уравнения всегда можно здесь. Далее стоит изучить теорему Виета, понять, а как возникает формула для дискриминанта, как быть с уравнением третьей степени.
Полный пример решения квадратного уравнения.
Условие
Решить уравнение 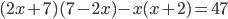
Решение
Согласно алгоритму, раскрываем скобки: 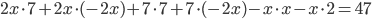 .
.
На всякий случай, расписал все подробно. Но вообще такие действия надо научиться делать почти устно. Более того, лучше заметить, что к первому слагаемому применима формула сокращенного умножения, точнее, разность квадратов. Такие формулы позволяют значительно экономить время и силы (потренироваться можно здесь).
Но продолжим решение: 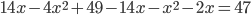 . Приводим подобные слагаемые и переносим
. Приводим подобные слагаемые и переносим 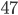 в левую часть уравнения:
в левую часть уравнения: 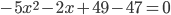
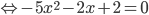 .
.
Изменим знак  :
: 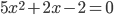 .
.
Находим дискриминант. Так как 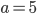 ,
, 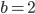 и
и 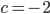 , то
, то 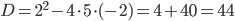 . Дискриминант
. Дискриминант 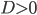 , поэтому у уравнения два корня:
, поэтому у уравнения два корня: 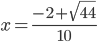 и
и 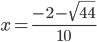 .
.
Осталось заметить, что корни можно упростить, ведь 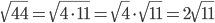 .
.
Получаем окончательный ответ, который запишем одной формулой: 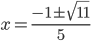 .
.
Как видите, малейшая неточность в арифметических вычислениях - и весь труд в итоге напрасен.
Поэтому стоит потренироваться выполнять арифметические вычисления устно и без ошибок.
Ответ: 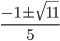
Задачи для самостоятельного решения
Номера 41, 42, 43, 51, 52, 53 (ответы находятся после условий)